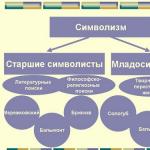
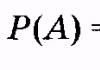Цель работы
- 1. Ознакомиться с методами построения кинетических моделей гетерогенных химических реакций.
- 2. Составить кинетическую модель гетерогенной химической реакции в соответствии с заданным механизмом.
- 3. Выбрать численный метод и разработать программу расчета.
- 4. Исследовать динамику изменения концентраций реагирующих веществ реакции и промежуточных соединений.
Кинетика гетерогенных химических реакций
Основы гетерогенной химической кинетики заложены в работах Лэнгмюра, Темкина и др. . В этих работах сформулировано понятие идеального адсорбированного слоя, базирующееся на аналогии с представлениями гомогенной кинетики. Эта модель использует следующие предположения:
- 1) равноценность всех участков поверхности катализатора и независимость энергии хемосорбции от степени заполнения поверхности различными адсорбентами;
- 2) неизменность катализатора и независимость его свойств от состава реакционной смеси и ее воздействия на катализатор;
- 3) равновесное распределение энергии.
Формальным аналогом кинетического закона действующих масс для элементарных процессов на твердых поверхностях является закон действующих поверхностей (ЗДП) .
Согласно его первоначальной формулировке скорость химической реакции пропорциональна произведению поверхностных концентраций реагирующих веществ в степенях, равных стехиометрическим соотношениям, в которых они вступают во взаимодействие (1.38).
Пусть протекает элементарная химическая реакция
При этом все вещества вступают во взаимодействие из адсорбированного состояния. Обозначим zi - долю поверхности, занятой i-м адсорбированным веществом. Тогда, в соответствии с законом действующих поверхностей, скорость необратимой реакции (1.38) можно записать как

где W - скорость химической реакции;
k - константа скорости; - доля поверхности, занятой i-й адсорбированной частицей; - доля свободной поверхности; i - стехиометрические коэффициенты стадий;
Изменение числа молей при протекании химической реакции.
Если не все вещества вступают во взаимодействие из адсорбированного состояния, а реагируют непосредственно из газовой фазы, то в более общем виде выражение закона действующих поверхностей записывается следующим образом:

где - парциальные давления (концентрации) -веществ, реагирующих из газовой фазы; - стехиометрические коэффициенты;
n, m - количество веществ, адсорбированных на поверхности катализатора и реагирующих из газовой фазы.
Пример: пусть протекает адсорбция водорода на активном центре катализатора Z с образованием адсорбированного поверхностного соединения ZH2:
тогда на основании ЗДП скорость данной элементарной химической реакции можно записать как
В качестве основного фактора, определяющего кинетические зависимости, вначале рассматривался фактор вытеснения, «борьбы» компонентов реакционной смеси за места на поверхности катализатора. При этом принималось дополнительное предположение о высокой скорости адсорбционных и десорбционных стадий по сравнению с собственно химическими превращениями. Последующие исследования показали существенную ограниченность этих предположений. Тем не менее Хиншельвудом, Швабом, Хоугеном, Ватсоном и другими на их основе получены уравнения, удовлетворительно описывающие кинетический эксперимент в определенном интервале изменения параметров. Типовая формула кинетического уравнения

где k - константа скорости;
Сi - концентрация i-го реагента газовой среды;
Константа равновесия стадии адсорбции i-го компонента;
i - стехиометрический коэффициент.
Наиболее общее описание кинетики сложных реакций дано в теории стационарных реакций Хориути - Темкина .
Дзюро Хориути ввел следующие понятия: независимые промежуточные вещества, стехиометрическое число, маршрут реакции, независимые маршруты реакции.
Стехиометрические числа - это числа, выбранные таким образом, что после умножения химических уравнений каждой стадии на соответствующее стехиометрическое число и последующего сложения уравнений все промежуточные вещества сокращаются. Получаемое при этом уравнение называется брутто-уравнением. Каждый набор стехиометрических чисел, приводящий к исключению промежуточных веществ, называется маршрутом реакции.
В теории стационарных реакций вводятся понятия «пробег стадии», «пробег по маршруту» и «скорость реакции по базисному маршруту». Под числом пробегов стадии понимается разность числа актов элементарной реакции в прямом и обратном направлениях. Тогда скорость простой реакции равна числу ее пробегов за единицу времени в единичном реакционном пространстве. Один пробег по маршруту означает, что произошло столько пробегов каждой из стадий, каково ее стехиометрическое число для данного маршрута. В том случае, когда образование молекулы промежуточного вещества в одной из стадий скомпенсировано расходованием этой молекулы в иной стадии, реализуется стационарный режим реакции. Если в ходе этой стадии образуется не конечный продукт, а новое промежуточное вещество, то и оно должно расходоваться в другой стадии. Полная компенсация образования и расходования промежуточных веществ и означает завершение пробега по какому-либо из маршрутов.
Таким образом, скорость стационарной реакции определяется отдельными пробегами по всевозможным маршрутам. В результате все пробеги стадий за данное время окажутся однозначно определенными через базисные маршруты. Скоростью реакции по базисному маршруту называется число пробегов по базисному маршруту в единицу времени в единичном реакционном пространстве при условии, что все пробеги стадий распределены по маршрутам данного базиса. Скорость реакции в целом задается скоростями по базисным маршрутам.
Условие стационарности элементарных стадий химических реакций можно записать следующим образом:
где - скорости элементарных стадий (s-й, прямой и обратной); - скорость по маршруту Р;
Стехиометрический коэффициент s-й стадии, маршрута Р.
На основании уравнения (1.44) получим уравнение, которое называется уравнением стационарных реакций:

где, ... - скорости по маршрутам;
Скорости элементарных стадий в прямом и обратном направлениях;
Стехиометрический коэффициент i-й стадии по j-му маршруту.
С помощью данного уравнения облегчается вывод кинетических уравнений для гетерогенных химических реакций в явном виде - для линейных механизмов и в некоторых случаях - для нелинейных.
^ Матричный метод
Помимо метода направленных графов существуют и другие методы решения стехиометрических задач для сложных систем химических реакций. Матричный метод позволяет свести задачу к такой форме, которая в наибольшей степени пригодна для дальнейшего ее решения с использованием компьютерной техники.
Рассмотрим решение предыдущей задачи с использованием матричного метода. В системе из 4 химических реакций принимают участие 7 веществ. Уравнения химических реакций с участием этих веществ можно записать так, как если бы в них участвовали все вещества одновременно. Если в какой-то химической реакции вещество не принимает участия, формально это означает, что стехиометрический коэффициент при этом веществе равен нулю. Условимся также, что стехиометрические коэффициенты для исходных веществ будем принимать положительными, а для продуктов – отрицательными. Тогда первое из химических уравнений системы химических реакций, рассмотренных в предыдущем примере, может быть записано следующим образом:
A + 2B - 2C + 0D + 0E + 0F + 0H = 0.
Рассуждая аналогично для всех веществ и всех реакций составим систему линейных уравнений, описывающих соотношение масс всех участвующих в реакциях веществ. Размерность системы 4х7, где 4- число уравнений, 7- число веществ, участвующих в химических реакциях. Матрица коэффициентов этих уравнений приведена ниже, а вектор-столбец нулевой.
К полученной системе уравнений необходимо добавить еще несколько уравнений, имеющих не нулевую правую часть. Эти уравнения записываются исходя из начальных условий задачи.
A B C D E F H
1 2 -2 0 0 0 0 0
1 0 0 -2 0 0 0 0
0 0 1 -1 0 -1 0 0
0 0 0 1 0 -2 -1 0
При определённых условиях, когда известны значения исходных и текущих масс некоторых компонентов системы, можно получить единственное решение методами линейной алгебры.
Описание систем путём расчёта стехиометрии химических реакций с практической точки зрения позволяет рассчитать массы всех участвующих веществ. Таким образом, можно прогнозировать поведение системы, состав продуктов, количество израсходованных веществ.
Стехиометрические расчёты предполагают, что все химические реакции в данном технологическом процессе идут до конца вправо.
^ Моделирование равновесия в системах химических реакций
Значительная часть химических реакций, составляющих основное содержание технологических процессов в цветной металлургии, являются обратимыми. Рассмотрим пример обратимой химической реакции:
Равновесие в такой химической реакции достигается при определенных значениях активностей участвующих веществ. Если эти вещества находятся в растворе, а их концентрации невелики (разбавленные растворы), то с некоторым приближением вместо величин активностей можно использовать величины концентраций. Равновесие в химической реакции характеризуется величиной константы равновесия:
 .
.
Величина константы равновесия связана с изменением энергии Гиббса и может быть рассчитана по термодинамическим данным участвующих веществ:

где Δ G T - изменение энергии Гиббса для данной химической реакции, Т – температура, R - универсальная газовая постоянная.
Рассчитав величину константы равновесия для химической реакции, идущей при заданной температуре, можно определить соотношение концентраций исходных веществ и продуктов, которое установится при достижении равновесия.
Несколько более сложно определить равновесный состав системы, в которой одновременно происходит несколько обратимых химических реакций. Рассмотрим следующий пример. Пусть имеется система обратимых химических реакций с участием веществ А, В, С и D. В данной системе вещество А последовательно и обратимо превращается в вещество С, предварительно образуя В. Возможен и параллельный путь: вещество А параллельно с образованием В разлагается с образованием D. При заданных условиях (температуре, давлении) в системе установится равновесие и будут достигнуты равновесные концентрации веществ.
Для расчета равновесных концентраций запишем выражения для констант равновесия всех реакций через равновесные концентрации:
А В  ;
; 
В С  ;
;
А D  ;
;  .
.
Пусть в начальный момент отсутствуют промежуточные вещества В и С, а также конечный продукт D:
 ; С В0 =0; С С0 =0; C D 0 =0.
; С В0 =0; С С0 =0; C D 0 =0.
Значения констант равновесия рассчитаем для каждой из реакций по термодинамическим данным:  . Таким образом, величины констант равновесия будем считать известными величинами.
. Таким образом, величины констант равновесия будем считать известными величинами.
На единицу объёма данной системы С А0 – С А представляет собой количество израсходованных молей компонента А. В соответствии со стехиометрией химических реакций и законом сохранения вещества, убыль массы А равна сумме масс образующихся веществ B,C и D, что можно выразить уравнением:
С А0 – С А = C B + C C + C D .
Преобразуем уравнение к следующему виду:
C A0 = C A + C B + C C + C D ,
И подставим в правую часть выражения для соответствующих концентраций веществ:
C A0 = C A + k 1 C A + k 1 k 2 C A + k 3 C A .
Сгруппируем однородные члены уравнения
C A 0 = C A (1 + k 1 + k 1 k 2 + k 3)
и получим выражение для равновесной концентрации С А
 .
.
Равновесные концентрации других веществ легко определить, поскольку значения всех констант равновесия нам известны из предыдущего расчета, а выражения содержат C A .
При расчётах равновесий в системах химических реакций необходимо знать k р каждой реакции, начальный состав системы – это даёт возможность рассчитать равновесный состав системы.
Реальные задачи расчёта равновесного состава систем намного сложнее: уравнения в этих задачах нелинейны; требуется учесть, что компоненты, входящие в реакцию находятся в разных фазах; вместо концентраций корректно использовать значения активностей компонентов. Практический смысл расчёта равновесий в таких сложных системах сводится к тому, что расчётный равновесный состав системы является тем физико-химическим пределом, до которого может дойти реальный процесс, если для его осуществления отведено неограниченное время.
^ Моделирование кинетики химических реакций
В физической химии скорость химической реакции определяется в соответствии с уравнением:
 ,
,
где dq – изменение массы реагирующего вещества, моль.
dt – приращение времени, с.
V – мера реакционного пространства.
Различают гомогенные химические реакции, в которых все участвующие вещества находятся в пределах одной фазы (газовой или жидкой). Для таких реакций мерой реакционного пространства является объем, а размерность скорости будет:  .
.
Гетерогенные химические реакции происходят между веществами, находящимися в разных фазах (газ-твердое, газ-жидкость, жидкость-жидкость, твердое-жидкость). Собственно химическая реакция при этом реализуется на поверхности раздела фаз, которая и является мерой реакционного пространства.
Для гетерогенных реакций размерность скорости иная:  .
.
Изменение массы реагирующих веществ имеет свой знак. Для исходных веществ масса по ходу реакции убывает, изменение массы имеет отрицательный знак, и величина скорости принимает отрицательное значение. Для продуктов химической реакции масса возрастает, изменение массы положительно, знак скорости принимают также положительным.
Рассмотрим простую химическую реакцию
А + 2В = 2С.
К простым реакциям относятся те, которые осуществляются в одну стадию и идут до конца, т.е. являются необратимыми.
Определим скорость такой химической реакции. Для этого прежде всего необходимо решить, по какому из веществ будет определена скорость реакции: ведь А и В – исходные вещества, и изменение их масс отрицательно, а С является конечным продуктом, и его масса возрастает со временем. Кроме того, не все стехиометрические коэффициенты в реакции равны единице, а это значит, что если расход А за какое-то время равен 1 молю, расход В за это же время будет 2 моля, и соответственно значения скорости, рассчитанные по изменению масс А и В будут отличаться вдвое.
Для простой химической реакции можно предложить единую меру скорости, которая определяется следующим образом:
 ,
,
где r i – скорость по i-му участнику реакции
S i – стехиометрический коэффициент i-го участника реакции.
Стехиометрические коэффициенты для исходных веществ принимаются положительными, для продуктов реакции они отрицательны.
Если реакции идут в изолированной системе, не обменивающейся веществом с внешней средой, то только химическая реакция приводит к изменению масс вещества в системе, и, следовательно, их концентраций. В такой системе единственной причиной изменения концентраций С является химическая реакция. Для этого частного случая
 ,
,
Скорость химической реакции зависит от концентраций участвующих веществ и от температуры.

где k – константа скорости химической реакции, С А ,С В – концентрации веществ, n 1 , n 2 – порядки по соответствующим веществам. Это выражение известно в физической химии как закон действующих масс.
Чем выше значения концентраций, тем выше скорость химической реакции.
Порядок (n ) определяется экспериментально и связан с механизмом химической реакции. Порядок может быть целым или дробным числом, существуют также реакции нулевого порядка по каким-то веществам. Если порядок по i -му веществу равен нулю, то скорость химической реакции не зависит от концентрации этого вещества.
Значение скорости химической реакции зависит от температуры. В соответствии с законом Аррениуса константа скорости изменяется при изменении температуры:

где ^ А – предэкспоненциальный множитель;
Е – энергия активации;
R – универсальная газовая постоянная, константа;
Т – температура.
Как и величина порядка реакции, величины энергии активации и предэкспоненциального множителя определяются для конкретной реакции экспериментально.
Если химическая реакция осуществляется в гетерогенном процессе, то на её скорость оказывает влияние так же процесс подвода исходных веществ и отвода продуктов из зоны химической реакции. Таким образом, имеет место сложный процесс, в котором имеются диффузионные стадии (подвод, отвод) и кинетическая стадия – собственно химическая реакция. Скорость всего процесса в целом, наблюдаемого в эксперименте, определяется скоростью самой медленной стадии.
Таким образом, влияя на скорость диффузионной стадии процесса (перемешивание), влияем на скорость всего процесса в целом. Это влияние сказывается на величине предэкспоненциального множителя А.
Большинство химических реакций не являются простыми (т.е. идут не в одну стадию и не до конца) – сложные химические реакции:
А) AB – обратимые;
Б) А→В; В→С – последовательные;
В) А→В; А→С – параллельные.
Для сложной химической реакции нет единой меры скорости . В отличие от простой, здесь можно говорить о скорости образования и разрушения каждого химического вещества. Таким образом, если в системе происходят химические реакции и участвуют n веществ, для каждого из n веществ есть своё значение скорости.
Для любого из веществ скорость образования и разрушения является алгебраической суммой скоростей всех стадий с участием этого вещества.
Скорость сложной химической реакции
Моделирование кинетики системы сложных химических реакций рассмотрим на следующем примере. Пусть имеется технологический процесс, суть которого отображается следующими химическими реакциями:
K 1 ; 1 по В
K 2 ; 0,7 по С
K 3 ; 1 по А; 0,35 по Н
K 4 ; 1 по С; 1 по D
K 5 ; 2 по Е;
R A = –k 1 C B + k 2 C C 0.7 – k 3 C A C H 0.35
R B = –2k 1 C B + 2k 2 C C 0.7
R C = k 1 C B – k 2 C C 0.7 – k 4 C C C D + k 5 C E 2
R D = k 3 C A C H 0.35 – k 4 C C C D + k 5 C E 2
R E = k 4 C C C D – 3k 5 C E 2
Кинетические константы (порядки по веществам и значения констант скорости для стадий) определены экспериментально. На схеме процесса над стрелками, соответствующими стадиям, показаны величины порядков по веществам. Не указанные порядки нулевые.
В процессе принимают участие 6 веществ: А и В являются исходными, С и D – промежуточными, Е – конечный продукт, Н – катализатор одной из стадий. Три химические реакции имеют пять стадий, три из которых являются прямыми, две – обратными.
Все реакции осуществляются гомогенно и проходят в замкнутой по веществу системе, что дает основания использовать для характеристики скорости выражения:
 .
.
На основании изложенного выше запишем выражения для скоростей по каждому веществу-участнику. Всего получим 6 выражений по числу веществ. Для каждого из веществ скорость расходования или образования есть алгебраическая сумма скоростей всех стадий с участием данного вещества. Так, веществ А участвует в трех стадиях, в первой в качестве исходного вещества, во второй- как продукт, в третьей вновь как исходное вещество. Слагаемые скорости для первой и третьей стадий будут отрицательны, для второй стадии скорость имеет положительный знак. Значения скорости для каждой стадии по закону действующих масс являются произведением константы скорости соответствующей стадии и концентраций веществ в степенях, равных порядкам по веществам. С учетом этого выражения для скоростей по веществам будут следующими:
 = –k 1 C B + k 2 C C 0.7 – k 3 C A C H 0.35
= –k 1 C B + k 2 C C 0.7 – k 3 C A C H 0.35
 = –2k 1 C B + 2k 2 C C 0.7
= –2k 1 C B + 2k 2 C C 0.7
 = k 1 C B – k 2 C C 0.7 – k 4 C C C D + k 5 C E 2
= k 1 C B – k 2 C C 0.7 – k 4 C C C D + k 5 C E 2
 = k 3 C A C H 0.35 – k 4 C C C D + k 5 C E 2
= k 3 C A C H 0.35 – k 4 C C C D + k 5 C E 2
 = 3k 4 C C C D – 3k 5 C E 2
= 3k 4 C C C D – 3k 5 C E 2
 = 0.
= 0.
Последняя скорость по веществу Н, катализатору третьей стадии, равна нулю. Масса катализатора не изменяется по ходу реакции.
В левой части всех уравнений присутствует производная концентрации вещества по времени, следовательно, уравнения кинетики являются дифференциальными. Концентрации в правой части уравнений в произвольный момент времени должны одновременно удовлетворять всем уравнениям, а это означает, что совокупность уравнений кинетики в математическом смысле есть система уравнений.
Модель химической кинетики является системой дифференциальных уравнений , решением которой является набор функций C i = f i (t ) :
С А =f 1 (t)
Для того, чтобы установить конкретный вид функций, необходимо решить систему дифференциальных уравнений, т.е. проинтегрировать систему уравнений кинетики. Интегрирование уравнений кинетики рассмотрим ниже на более простом примере, а после этого вновь вернемся к задаче, рассмотренной выше.
^ Интегрирование уравнений кинетики
Пусть идет химическая реакция разложения вещества А, в результате которой образуется вещество В. Экспериментально установлено, что она имеет первый порядок по концентрации А, а значение константы скорости для условий ее осуществления равно k. Это отображено на схеме реакции ниже.
k; 1 по А
Скорость реакции равна r a = –kC A , или
 .
.
Определим начальные условия для решения дифференциального уравнения кинетики. Будем считать, что в начальный момент реакции нам известна концентрация вещества А, обозначим ее как С Ао. Запишем начальные условия в виде  . Проинтегрируем полученное уравнение, используя интегралы с подстановкой пределов. Пределы интегрирования определяются из начальных условий: когда время равно нулю, концентрация А равна начальной, в произвольный момент t
концентрация равна С
А
:
. Проинтегрируем полученное уравнение, используя интегралы с подстановкой пределов. Пределы интегрирования определяются из начальных условий: когда время равно нулю, концентрация А равна начальной, в произвольный момент t
концентрация равна С
А
:
 .
.
В результате интегрирования имеем:
 ,
,
Заменяя разность логарифмов логарифмом частного имеем далее:
 ,
,
Проводя потенцирование получим:
 .
.
После всех преобразований решение дифференциального уравнения представляет собой экспоненциальную убывающую функцию:
 .
.
Проверим, не противоречит ли полученное решение условиям нашей задачи. При t = 0, т.е. в момент начала химической реакции С A = C A 0 , поскольку экспонента обращается в единицу. Действительно, в начальный момент концентрация вещества А равна начальной. При t →∞ экспонента с отрицательным показателем стремится по величине к нулю. За бесконечно большое время вследствие химической реакции все вещество разлагается и образует В.
^ Численные методы интегрирования
Вернемся теперь к предыдущей задаче. Очевидно, что интегрирование системы дифференциальных уравнений является более сложной задачей по сравнению с рассмотренной ранее. Применение аналитичееских приемов интегрирования вряд ли возможно, поскольку правые части дифференциальных уравнений содержат концентрации сразу нескольких веществ, и разделить переменные не удастся.
Воспользуемся численным методом интегрирования. Для этого разобьем ось времени на малые отрезки (шаги). Считая, что производные концентраций веществ по времени есть математический предел отношения приращений концентраций к приращению времени, при Δ t , стремящемся к нулю:
 ,
,
преобразуем систему дифференциальных уравнений в систему алгебраических. В левой части приращение времени нам известно, поскольку шаг по времени мы выбираем сами. Важно только то, что этот шаг должен быть малым.
В правой части значения всех констант скорости нам также известны из эксперимента, то же следует сказать и о величинах порядков. Подставим в правую часть также значения концентраций всех веществ, воспользовавшись начальными условиями. Каждое из уравнений системы содержит в этом случае лишь одну неизвестную величину – изменение концентрации Δ C i . По сути это изменение концентрации за первый шаг решения, когда время изменяется от нуля (начала химической реакции) до Δ t . Изменение концентрации со своим знаком суммируем с начальной концентрацией и определяем концентрацию каждого из веществ на момент окончания первого шага решения.
На следующем шаге решения в правую часть подставим значения концентраций из предыдущего шага решения и вновь получим Δ C i , но теперь для следующего шага решения, как показано на рисунке.
На каждом шаге решения получаем ординаты, соответствующие изменению концентрации всех веществ, участвующих в реакциях. Геометрическое место точек, являющихся ординатами, даст для каждого из веществ график функции изменения концентрации во времени. Заметим, что в результате численного интегрирования мы не получаем аналитического выражения, задающего изменение концентрации во времени, ординаты на графике получаются расчетным путем. Однако построение графиков функций изменения концентраций по времени возможно, а вид кривых позволяет сделать ряд выводов, имеющих практический смысл.
Очевидно, что концентрации исходных веществ со временем убывают, поскольку они расходуются в реакции. Не менее очевидно, что концентрации конечных продуктов возрастают.
Поведение промежуточных веществ заслуживает отдельного рассмотрения. Графики концентраций промежуточных веществ имеют максимумы, соответствующие определенной продолжительности реакции. Если промежуточное вещество является целевым продуктом химических реакций, то максимум концентрации соответствует оптимальной продолжительности для получения данного целевого вещества.
Так происходит потому, что в начальный момент химической реакции концентрации исходных веществ велики, а скорость химической реакции с участием исходных веществ пропорциональна их концентрациям. Реакции с участием исходных веществ вначале происходят с большими скоростями. Это означает, что промежуточные вещества образуются также с высокой скоростью.
С другой стороны, скорость разложения промежуточных веществ также пропорциональна их концентрации, и мала вначале. Скорость образования промежуточных веществ больше скорости их разложения, что способствует накоплению промежуточных веществ, их концентрация возрастает.
По мере развития химической реакции уменьшается скорость образования промежуточных веществ и растет скорость их разрушения. Когда величины скоростей становятся одинаковыми, рост концентрации прекращается, в системе наблюдается максимум концентрации промежуточного вещества.
Далее скорость образования промежуточного вещества снижается, поскольку продолжается уменьшение концентраций исходных веществ. Скорость разрушения промежуточного вещества также уменьшается, оставаясь по величине больше скорости образования, а это приводит к расходованию промежуточного вещества в системе и к падению его концентрации.

 ;
;
Т С – оптимальное время для получения вещества С.
Рассмотрим поведение вещества С: в начальный момент времени С С = 0.
K 1 C B >k 2 C C 0.7
Таким образом, моделирование кинетики позволяет определить образование и расходование всех веществ в системах химических реакций, установить вид функции концентрации в зависимости от времени, в ряде случаев определить оптимальные условия по ведению химической реакции.
^ Химические реакции в потоке вещества
Многие технологические аппараты работают в непрерывном режиме. Рассмотрим в качестве примера плавильную печь для переработки шихты из медных концентратов и флюсов. Схема такого аппарата приведена ниже на рисунке.
Н епрерывный проточный аппарат представляет собой проточный реактор, в котором осуществляется определённый набор химических реакций.
епрерывный проточный аппарат представляет собой проточный реактор, в котором осуществляется определённый набор химических реакций.
Наличие потоков вещества влияет на условия осуществления химических реакций.
Реальные потоки вещества обладают достаточно сложными свойствами:
гидродинамический режим – ламинарный, турбулентный, переходный;
число фаз – много- и однофазные.
Примером является поток, движущийся по трубе. Скорость движения потока в пределах одного сечения неодинакова: наибольшее значение скорости на оси потока, а вблизи стен за счет торможения потока силами вязкости эта скорость мало отличается от нуля. Однако, если объемный расход среды потока равен Q, а площадь сечения F, нетрудно определить среднюю скорость течения потока, равную Q/F.
 Q м 3 /c
Q м 3 /c

Еще больше сложностей возникает при описании многофазных потоков, а реальные потоки как раз чаще всего ими и являются.
В этой связи учитывать свойства реальных потоков при создании математической модели достаточно сложно. Поэтому для создания модели аппаратов проточного типа существует несколько идеализированных моделей течения потоков.
^ 1. Модель идеального вытеснения – такая идеализированная модель потока основана на следующих допущениях (аппаратом такого типа может быть трубчатая обжиговая печь):
поток стационарный, объемный расход среды не меняется во времени;

в таком потоке скорости во всех точках потока одинаковы;
элемент объёма dV в таком потоке является замкнутой по веществу системой (не обменивается с соседними элементами);
в потоке идеального вытеснения отсутствует продольное перемешивание;
поперечное перемешивание в потоке тоже отсутствует.
Для моделирования кинетики в случае потока идеального вытеснения вполне годится подход, применимый к системам, изолированным по веществу.
Рассмотрим реакцию первого порядка, которая проходит в аппарате идеального вытеснения.
K 1 ; 1 по А
С оздадим модель, позволяю-щую рассчитать выходную концен-трацию А. Константа известна, поря-док первый.
оздадим модель, позволяю-щую рассчитать выходную концен-трацию А. Константа известна, поря-док первый.



 – время пребывания вещества в аппарате
– время пребывания вещества в аппарате


Чем больше константа скорости k , тем быстрее концентрация стремится к концентрации в точке выхода.
В пределах аппарата идеального вытеснения концентрация вещества не остаётся постоянной – она падает от концентрации в точке входа до концентрации в точке выхода.
^ 2. Модель идеального перемешивания (аппаратом такого типа является, например, печь КС, гидрометаллургический реактор для выщелачивания и т.п.).
Допущения:
поток стационарный, объёмный расход вещества (Q) через аппарат должен быть постоянным;
концентрация во всех точках аппарата идеального перемешивания одинакова.
 ледствием второго допущения является то, что концентрация вещества в точке выхода равна концентрации внутри аппарата.
ледствием второго допущения является то, что концентрация вещества в точке выхода равна концентрации внутри аппарата.
Среднее время пребывания вещества в аппарате –  .
.
Время пребывания различных порций потока в аппарате идеального перемешивания неодинаково.
Элемент объёма в таком аппарате является открытой системой, для такого аппарата не годится подход для замкнутой системы. Для описания кинетики в этом случае используем закон вещества и рассматриваем аппарат, как единое целое, концентрация во всех точках одинакова. На основании закона сохранения вещества запишем уравнение материального баланса для всего аппарата в целом (в единицу времени):
Приход – Расход = 0
Пусть в условиях аппарата идеального перемешивания происходит реакция разложения первого порядка:
K 1 ; 1 по А
Материальный баланс по веществу А будет суммой составляющих:
1 слагаемое – число молей вещества А, вносимое потоком в единицу времени;
2 слагаемое– унос вещества из аппарата в единицу времени;
3 слагаемое– масса вещества, израсходованного в химической реакции. Разделим обе части уравнения на величину объемного расхода Q≠0:

 .
.
Создадим для химических реакций одинаковые условия в том и другом аппарате (одинаковая температура,  k 1 =k 2). Допустим, что при определённой температуре k 1 =k 2 =1. зададим С А0 = 1 моль/м 3 . Vа = 1м 3 , Q 1 = Q 2 = 1м 3 /с. Тогда:
k 1 =k 2). Допустим, что при определённой температуре k 1 =k 2 =1. зададим С А0 = 1 моль/м 3 . Vа = 1м 3 , Q 1 = Q 2 = 1м 3 /с. Тогда:

 .
.
Удивительно то, что результат одной и той же химической реакции оказывается в разных аппаратах разным. Более эффективным является аппарат идеального вытеснения, в котором выходная концентрация оказывается ниже.
Причиной этого является не скорость химической реакции (она одинакова в обоих аппаратах), а наличие или отсутствие перемешивания элементов потока. В аппарате идеального перемешивания на выходе установится концентрация, являющаяся результатом перемешивания порций вещества, находившихся внутри аппарата в течение разного времени. Некоторые порции вещества проскакивают аппарат быстро, и продолжительность реакции в таких порциях мала, а концентрация вещества А, напротив, высока. Другие порции вещества находятся внутри аппарата достаточно долго, продолжительность химической реакции велика, а остаточная концентрация А - мала.
^ Ячеечная модель потока . Согласно этой модели, реальный технологический аппарат заменяется идеализированной схемой – последовательность ячеек идеального перемешивания.
 1 ; 1 по А
1 ; 1 по АП усть n=2, тогда на выходе 1-й ячейки:
усть n=2, тогда на выходе 1-й ячейки:

Если n ячеек, то 
Учитывая, что  – переходим к решению для аппарата идеального вытеснения. При n=1 имеем очевидное решение для аппарата идеального перемешивания.
– переходим к решению для аппарата идеального вытеснения. При n=1 имеем очевидное решение для аппарата идеального перемешивания.
Покажем на графиках, как увеличение количества ячеек может позволить нам перейти с помощью ячеечной модели от аппарата идеального перемешивания к аппарату идеального вытеснения.

Ч тобы исключить продольное перемешивание в потоке, рабочий объём аппарата секционируют.
тобы исключить продольное перемешивание в потоке, рабочий объём аппарата секционируют.
Применяют также каскадирование аппаратов – последовательное соединение технологических аппаратов для выравнивания результатов химических реакций.
Моделирование кинетики в потоках химических реакций позволяет, учитывая особенности потока, рассчитать характеристики работы оборудования (выходной состав).
Математическое описание перечисленных выше физико-химических процессов имеет большое значение при создании динамических моделей, воспроизводящих поведение процессов во времени. Такие модели позволяют прогнозировать будущее состояние процесса, определять оптимальные траектории его протекания, а следовательно, и пути повышения производительности или экономичности. При этом открывается также возможность автоматизации управления с использованием ЭВМ.
Особенности кинетики гомогенных и гетерогенных реакций
Скорости протекания химических реакций зависят от целого ряда факторов: концентрации реагирующих веществ, температуры, давления (если в реакции участвуют газообразные вещества), наличия катализаторов, а в случае гетерогенных превращений, кроме того – от состояния поверхности, условий тепло- и массообмена. Рассмотрим, в связи с этим, особенности кинетики гомогенных и гетерогенных реакций. При гомогенных реакциях исходные вещества и продукты взаимодействия находятся в одной и той же фазе (газовой или жидкой), при этом молекулы, атомы или ионы могут взаимодействовать по всему занятому объему. Примером могут служить реакции горения и , входящих в состав коксового (природного) газа:
![]()
![]()
При гетерогенных реакциях взаимодействующие вещества находятся в различных фазах, а процесс химического превращения протекает на границе раздела этих фаз.
Реакция окисления углерода в системе шлак-металл, как пример гетерогенной реакции
Реакция
Примером может служить реакция окисления углерода в системе шлак – металл применительно к ванне мартеновской или электросталеплавильной печи

Три стадии реакции
Здесь можно выделить, по меньшей мере, три стадии:
- диффузия кислорода из шлака в металл к месту реакции (граница раздела: металл – газовый пузырь, незаполненные поры на подине или поверхности кусков руды и извести);
- химическая реакция между кислородом и углеродом металла на границе раздела упомянутых фаз;
- выделение газообразного продукта реакции из металла.
Следует заметить, что при более подробном анализе каждая из перечисленных стадий может быть разбита еще на несколько стадий, отражающих, в частности, адсорбционно-химические акты на границах раздела фаз (см. рис.1.3 – 1.5). Скорость такой сложной гетерогенной реакции лимитируется наиболее медленной стадией процесса. Для условий мартеновского и электросталеплавильного процессов такой стадией является диффузия кислорода из шлака в металл. В конвертерном процессе в связи с большой интенсивностью продувки кислородом и высокой степенью диспергирования взаимодействующих фаз лимитирующими могут оказаться адсорбционно-химические акты на поверхности раздела фаз, величина которой возрастает на несколько порядков по сравнению с подовыми сталеплавильными процессами.
Описание диффузии и массопереноса
Диффузия
Прежде чем продолжить описание кинетики, остановимся на закономерностях диффузии, которая имеет большое значение при гетерогенных процессах, так как их скорости могут определяться подводом реагирующих веществ и отводом продуктов реакции.
Диффузия есть процесс самопроизвольного перемещения вещества, направленный на выравнивание концентраций в объеме. Движущейся силой диффузии является градиент концентрации , определяемый изменением концентрации вещества , приходящегося на отрезок пути в направлении диффузии. Приращение количества переносимого путем диффузии вещества пропорционально коэффициенту диффузии , градиенту концентрации, площади поперечного сечения среды, через которую переносится вещество, и времени .
![]() а переходя к бесконечно малым приращениям и скорости диффузии (потоку массы через единичную площадь)
а переходя к бесконечно малым приращениям и скорости диффузии (потоку массы через единичную площадь)
![]() получаем уравнение
получаем уравнение
![]() (3.57) описывающее стационарную диффузию и называемое первым законом Фика.
(3.57) описывающее стационарную диффузию и называемое первым законом Фика.
Диффузия системы с распределёнными параметрами позакон Фика
Для случая системы с распределенными параметрами, когда концентрация изменяется по всем трем координатам, в соответствии со вторым законом Фика уравнение диффузии принимает следующий вид:
![]() (3.58) где – плотность источников вещества, например, количество вещества, образующегося в результате химических реакций в единице объема в единицу времени.
(3.58) где – плотность источников вещества, например, количество вещества, образующегося в результате химических реакций в единице объема в единицу времени.
Условия применимости молекулярной диффузии
Необходимо подчеркнуть, что уравнения (3.57) и (3.58) относятся к молекулярному переносу в неподвижной среде и справедливы для изотермического процесса и случая, когда диффузия данного компонента не зависит от диффузии других компонентов.
Формула Стокса-Эйнштейна
В этих условиях зависимость коэффициента диффузии от температуры , вязкости среды и радиуса диффундирующих молекул определяется формулой Стокса – Эйнштейна:
![]() (3.59) где
(3.59) где
И – газовая постоянная и число Авогадро.
Турбулентная диффузия
В большинстве металлургических агрегатов, особенно сталеплавильных, преобладающую роль играет не молекулярная, а турбулентнаядиффузия , обусловленная тепловой конвекцией и работой перемешивания поднимающихся пузырей и внедряющихся в ванну струй продувочного газа.
Например, значение коэффициента атомарной диффузии в неподвижном расплавленном железе при 1500 – 1600°C составляет – . Величина же коэффициента турбулентной диффузии в мартеновской ванне, зависящая от скорости обезуглероживания, составляет 0,0025 -0,0082 , а в конвертерном процессе 2,0 -2,5, т. е. на три порядка выше.
Диффузия с учетом влияния конвекции
С учетом влияния конвекции уравнение диффузии принимает следующий вид:
![]() (3.60) где – скорость переноса вещества, м/с.
(3.60) где – скорость переноса вещества, м/с.
Чаще, в случаях преобладающего влияния турбулентной диффузии, используется эмпирическое уравнение вида
– диффузионный поток;
– разность концентраций;
– коэффициент массоотдачи (турбулентной диффузии).
Эмпирическое уравнение для турбулентной диффузии
При оценке условий массопереноса и возможных областей использования приведенных выше уравнений целесообразно воспользоваться методами теории подобия , которая, как показано при анализе второй теоремыподобия , открывает возможность обобщений.
Прежде всего, следует заметить, что диффузия , вязкость и теплопроводность являются подобными процессами, характеризующими аналогичные виды переноса: диффузия – перенос массы, вязкость – перенос количества движения, теплопроводность – перенос тепла. Коэффициенты молекулярного переноса (вязкость , диффузия и температуропроводность ) имеют одинаковую размерность ().
Число Рейнольдса
В соответствии со второй теоремой подобия можно существенно снизить размерность задачи и повысить общность, если от первичных физических параметров перейти к их безразмерным комплексам, называемым критериями или числами подобия . Одним из таких широко известных критериев является число Рейнольдса , позволяющее оценивать характер движения жидкости в зависимости от ее средней скорости , диаметра трубопровода (потока) и кинематической вязкости :
(3.62) Этот критерий является мерой отношения сил инерции, характеризующихся скоростью, к силам внутреннего трения, характеризующихся вязкостью. Число Рейнольдса отражает степень устойчивости потока по отношению к внешним и внутренним возмущениям. Значение числа, при котором нарушается устойчивость движения жидкости, называется критическим и обозначается . При любые возникающие в потоке возмущения с течением времени затухают и не изменяют общего ламинарного характера течения. При возмущения могут самопроизвольно возрастать, что приводит к турбулизации потока. В действительности, резкой границы в переходе от ламинарного к турбулентному движению нет, имеется переходный режим, при котором в основной части потока преобладает турбулентный режим, а в слое, прилегающем к стенкам, возможно ламинарное движение.
При значении <2300 поток является ламинарным. В этой области для описания диффузии могут использоваться уравнения (3.57) или (3.60). Область значений 2300<<10000 является переходной. Здесь, в зависимости от степени развития турбулентности и наличия ламинарного слоя, целесообразно использовать уравнения (3.60) или (3.61).
При значениях >10000 в результате преобладающего влияния сил инерции поток становится турбулентным. В этих условиях пользоваться уравнениями, в которых фигурируют коэффициенты молекулярной диффузии, неправомерно. При таком характере потока для описания массопереноса используют уравнения вида (3.61), в которых коэффициент массоотдачи определяется либо через работу перемешивания, либо экспериментально -статистическими методами по измеренной скорости процесса и перепадам концентраций.
Уравнения кинетики гомогенных реакций
Скорость реакции
Скорость реакции представляет собой производную от концентрации по времени
Молекулярность реакции
Химические реакции различаются по признаку молекулярности и порядка реакции. Молекулярность определяется числом молекул, участвующих в элементарном акте химического взаимодействия. По этому признаку реакции делятся на моно-, би- и тримолекулярные. Каждому типу химической реакции соответствуют определенные кинетические уравнения, выражающие зависимость скорости реакции от концентрации реагирующих веществ. В соответствии с закономерностями формальной кинетики, в том числе законом действующих масс, скорость какой-либо реакции вида
В прямом направлении пропорциональна концентрациям реагирующих веществ и представляется уравнением
![]() (3.63) где
(3.63) где
– константа скорости, имеющая смысл при .
Порядок реакции
Определение
Порядком реакции называется сумма показателей степени, в которых концентрации входят в кинетические уравнения. Приведенная выше реакция имеет, следовательно, третий порядок. В действительности реакции третьего порядка наблюдаются редко. Уравнения, подобные выражению (3.63), основаны на упрощенных представлениях о том, что реакции происходят при одновременном столкновении такого числа молекул, которые соответствуют сумме стехиометрических коэффициентов. Большинство же реальных реакций протекает по более сложным законам с образованием промежуточных продуктов. Поэтому уравнения типа (3.63) верны только для элементарных реакций, идущих в одну стадию, т. е. по виду стехиометрического уравнения нельзя определить порядок реакций, чаще всего его определяют экспериментально . С этой целью находят скорость реакции при постоянной температуре в зависимости от концентрации реагентов, по виду полученной зависимости (показателям степеней при концентрациях) можно судить о порядке реакции. Для этой цели можно воспользоваться одним из методов параметрической идентификации, рассматриваемых в гл. 5.
Остановимся на виде кинетических уравнений в зависимости от порядка реакции.
Реакция нулевого порядка
При реакциях нулевого порядка скорость постоянна во времени
(3.64) После интегрирования получаем
– постоянная интегрирования, имеющая смысл начальной концентрации при =0.
Таким образом, в рассматриваемом случае концентрация реагента линейно убывает во времени.
Реакция первого порядка
Реакция первого порядка схематически представляется следующим образом:
Кинетическое уравнение имеет вид:
![]() (3.65) а его решение
(3.65) а его решение
![]() показывает, что концентрация исходного компонента экспоненциально уменьшается во времени (рис. 3.2).
показывает, что концентрация исходного компонента экспоненциально уменьшается во времени (рис. 3.2).

Рис. 3.2 Изменение концентрации и ее логарифма во времени при реакциях первого порядка
Решение этого уравнения можно представить и в другом виде, более удобном для определения константы скорости реакции. В результате разделения переменных и выбора пределов интегрирования
При температуре
 получаем решение
получаем решение
![]() из которого можно выделить, что линейно зависит от времени. Если опытные данные укладываются на прямую линию (см. рис. 3.2), то это указывает на первый порядок реакции. По углу наклона прямой определяется величина .
из которого можно выделить, что линейно зависит от времени. Если опытные данные укладываются на прямую линию (см. рис. 3.2), то это указывает на первый порядок реакции. По углу наклона прямой определяется величина .
Реакция второго порядка
Схема реакции второго порядка имеет вид
Или, например,
А скорость реакции описывается уравнением
![]() (3.66) которое при одинаковых концентрациях принимает вид
(3.66) которое при одинаковых концентрациях принимает вид
![]() После разделения переменных и интегрирования соотношения
После разделения переменных и интегрирования соотношения
 получаем соотношение
получаем соотношение
![]() (3.67) которое может быть использовано для определения . Если начальные концентрации реагентов неодинаковы и равны соответственно и, а концентрация продукта в момент составляет , то получаем уравнение
(3.67) которое может быть использовано для определения . Если начальные концентрации реагентов неодинаковы и равны соответственно и, а концентрация продукта в момент составляет , то получаем уравнение
Логарифмирование которого дает
![]() (3.68)
(3.68)
Обратная реакция
Все приведенные выше кинетические уравнения относятся к реакциям, протекающим только в прямом направлении, т. е. в условиях, далеких от равновесия, что может, например, обеспечиваться за счет непрерывного отвода продуктов реакции. В общем случае может протекать и обратная реакция, тогда общая скорость для реакции вида
(3.69) По мере расходования реагентов и и образования продукта скорость прямой реакции уменьшается, а увеличивается. При суммарная скорость равна нулю, наступает равновесие. Тогда
![]() или
или
(3.70) т. е. константа равновесия равна отношению констант скоростей прямой и обратной реакции. В то же время соотношение (3.70) есть не что иное, как выражение закона действующих масс , полученное в данном случае через уравнение кинетики.
Влияние температуры на скорость химической реакции
Остановимся теперь на вопросе влияния температуры на скорость химических реакций. Зависимость константы скорости реакции от температуры впервые была эмпирически получена Аррениусом, а несколько позже нашла теоретическое подтверждение на основе механизма активных столкновений. В дифференциальной форме она имеет следующий вид:
– энергия активации.
После интегрирования, при условии, что , получаем
– постоянная, имеющая смысл логарифма константы скорости при бесконечной температуре ().
Это соотношение можно представить также в виде
![]() (3.73)
(3.73)
Энергия активации
Величину можно определить по тангенсу угла наклона прямой (3.72), построенной в координатах , для чего необходимо измерить константы скорости при различных температурах.
Физический смысл энергии активации и механизм химических реакций можно объяснить на основе теории активных столкновений.
Вероятность осуществления элементарной химической реакции зависит от природы реагирующих веществ (энергии связей) и от температуры, повышающей общий энергетический уровень хаотического движения молекул. На рис 3.3, где и – энергии активации прямой и обратной реакций, видно, что в результате экзотермической реакции, происходит снижение внутренней энергии системы на величину, равную тепловому эффекту реакции.

Рис. 3.3 К вопросу об энергии активации
Однако, на пути от исходного состояния в конечное система должна перейти определенный энергетический барьер, при этом, чем ниже барьер (меньше энергия активации), тем большая доля молекул в каждый данный момент оказывается способной вступить в реакцию и тем более высокой будет скорость реакции.
Более подробное изложение молекулярной кинетики, нашедшее дальнейшее развитие в теории переходного состояния, выходит за рамки данного пособия.
Взаимосвязь массопереноса и кинетики в гетерогенных реакциях
Наглядное представление о взаимосвязях массопереноса и кинетики в гетерогенных процессах дает приведенная на рис.3.4 схема обобщенной модели.

Поверхности раздела фаз
В первом случае процессы не сопровождаются изменениями химического состава в пограничном слое. Взаимодействие же на поверхности раздела многокомпонентных систем характеризуется, чаще всего, изменением состава пограничного слоя, при этом общая скорость процесса определяется скоростью выравнивания концентрации в пограничном слое, т. е. скоростью диффузии. Диффузионный пограничный слой представляет собой тонкий слой, прилегающий к каждой фазе двух- или многокомпонентной системы (рис. 3.6).

Рис. 3.6 Диффузионный пограничный слой
- – твердое вещество
- – диффузионный пограничный слой
- – жидкость
С увеличением интенсивности перемешивания уменьшается толщина этого слоя и, следовательно, уменьшается влияние диффузии на скорость всего процесса. Подобные явления наблюдаются при растворении кусков кокса и агломерата в доменных печах или кусков извести в сталеплавильных агрегатах.
В системах , для которых характерно последовательное протекание химических и физических процессов, скорость всего процесса определяется более медленной стадией. В связи с этим реакция может находиться в кинетической или в диффузионной области. Если скорость химической реакции и диффузии соизмеримы, процесс является сложной функцией кинетических и диффузионных явлений и считается протекающим в переходной области.
Стадии гетерогенных реакций
В большинстве случаев гетерогенные реакции протекают через ряд стадий, наиболее характерные из которых следующие:
- диффузия частиц исходных веществ к поверхности раздела фаз (реакционной зоне);
- адсорбция реагентов на поверхности;
- химическая реакция на поверхности;
- десорбция продуктов реакции на поверхности раздела фаз;
- диффузия этих продуктов от реакционной зоны вглубь одной из фаз.
Стадии 1 и 5 относятся к диффузионным, а стадии 2 – 4 к кинетическим.
Кинетическое сопротивление гетерогенной реакции
Наблюдаемое кинетическое сопротивление гетерогенной реакции, протекающей через ряд последовательных стадий, равно сумме кинетических сопротивлений ее стадий
![]() (3.74) где
(3.74) где
– константа скорости суммарного (наблюдаемого) процесса;
– константа скорости кинетической стадии;
– константа скорости (коэффициент диффузии) диффузионной стадии.
Стадия, имеющая наибольшее сопротивление, является лимитирующей.
Особенности процессов в кинетической области
Рассмотрим основные особенности процессов в кинетической области:
Первые три особенности могут наблюдаться и в случае нахождения процесса в переходной области. Четвертый признак является основным экспериментальным подтверждением нахождения процесса в кинетической области.
Особенности процессов в диффузионной области
Основные особенности процессов в диффузионной области:
- процесс первого порядка;
- слабая зависимость скорости процесса от температуры и от величины поверхности раздела фаз;
- 3) резкое влияние на скорость процесса гидродинамических и аэродинамических условий процесса.
Наиболее важным признаком нахождения процесса в диффузионной области являются первая и третья особенности.
Растворение извести как пример гетерогенного процесса
Рассмотрим в качестве примера процесс растворения извести в основном сталеплавильном шлаке, что имеет место в мартеновских, электросталеплавильных печах и конвертерах. Этот процесс, являющийся типично гетерогенным, зависит, прежде всего, от конвективных потоков, развивающихся в ванне, т. е. от мощности перемешивания, и состоит из следующих этапов: подвод составляющих шлака (, и др.) к поверхности кусков извести; проникновение растворителей в поры кусков извести, что облегчает переход оксида кальция в жидкую фазу в связи с образованием легкоплавких соединений; отвод этих продуктов, насыщенных , от поверхности кусков извести в объеме шлака. Подвод растворителей к поверхности кусков извести и отвод растворяющейся определяется закономерностями конвективной диффузии в пределах диффузионного пограничного слоя у поверхности кусков извести. Уравнение диффузии имеет вид.
Цель работы
1. Ознакомиться с методами построения кинетических моделей гетерогенных химических реакций.
2. Составить кинетическую модель гетерогенной химической реакции в соответствии с заданным механизмом.
3. Выбрать численный метод и разработать программу расчета.
4. Исследовать динамику изменения концентраций реагирующих веществ реакции и промежуточных соединений.
Кинетика гетерогенных химических реакций
Основы гетерогенной химической кинетики заложены в работах Лэнгмюра, Темкина и др. . В этих работах сформулировано понятие идеального адсорбированного слоя, базирующееся на аналогии с представлениями гомогенной кинетики. Эта модель использует следующие предположения:
1) равноценность всех участков поверхности катализатора и независимость энергии хемосорбции от степени заполнения поверхности различными адсорбентами;
2) неизменность катализатора и независимость его свойств от состава реакционной смеси и ее воздействия на катализатор;
равновесное распределение энергии.
Формальным аналогом кинетического закона действующих масс для элементарных процессов на твердых поверхностях является закон действующих поверхностей (ЗДП) .
Согласно его первоначальной формулировке скорость химической реакции пропорциональна произведению поверхностных концентраций реагирующих веществ в степенях, равных стехиометрическим соотношениям, в которых они вступают во взаимодействие (1.38).
Пусть протекает элементарная химическая реакция
При этом все вещества вступают во взаимодействие из адсорбированного состояния. Обозначим z i – долю поверхности, занятойi -м адсорбированным веществом. Тогда, в соответствии с законом действующих поверхностей, скорость необратимой реакции (1.38) можно записать как
|
|
где W – скорость химической реакции;
k – константа скорости;
 –доля поверхности,
занятой i
-й адсорбированной частицей;
–доля поверхности,
занятой i
-й адсорбированной частицей;
 –доля свободной
поверхности;
–доля свободной
поверхности;
i – стехиометрические коэффициенты стадий;
 – изменение числа
молей при протекании химической реакции.
– изменение числа
молей при протекании химической реакции.
Если не все вещества вступают во взаимодействие из адсорбированного состояния, а реагируют непосредственно из газовой фазы, то в более общем виде выражение закона действующих поверхностей записывается следующим образом:
|
|
где
 – парциальные давления (концентрации)
– парциальные давления (концентрации) -веществ,
реагирующих из газовой фазы;
-веществ,
реагирующих из газовой фазы;
 –стехиометрические
коэффициенты;
–стехиометрические
коэффициенты;
n ,m – количество веществ, адсорбированных на поверхности катализатора и реагирующих из газовой фазы.
Пример: пусть протекает адсорбция водорода на активном центре катализатора Z с образованием адсорбированного поверхностного соединения ZH 2:
В качестве основного фактора, определяющего кинетические зависимости, вначале рассматривался фактор вытеснения, «борьбы» компонентов реакционной смеси за места на поверхности катализатора. При этом принималось дополнительное предположение о высокой скорости адсорбционных и десорбционных стадий по сравнению с собственно химическими превращениями.
Последующие исследования показали существенную ограниченность этих предположений. Тем не менее Хиншельвудом, Швабом, Хоугеном, Ватсоном и другими на их основе получены уравнения, удовлетворительно описывающие кинетический эксперимент в определенном интервале изменения параметров.
Типовая формула кинетического уравнения, соответствующего этим предположениям, имела вид
|
|
где k – константа скорости;
С i – концентрацияi -го реагента газовой среды;
 –константа
равновесия стадии адсорбции i
-го
компонента;
–константа
равновесия стадии адсорбции i
-го
компонента;
i – стехиометрический коэффициент.
Наиболее общее описание кинетики сложных реакций дано в теории стационарных реакций Хориути – Темкина .
Дзюро Хориути ввел следующие понятия: независимые промежуточные вещества, стехиометрическое число, маршрут реакции, независимые маршруты реакции.
Стехиометрические числа – это числа, выбранные таким образом, что после умножения химических уравнений каждой стадии на соответствующее стехиометрическое число и последующего сложения уравнений все промежуточные вещества сокращаются. Получаемое при этом уравнение называется брутто-уравнением . Каждый набор стехиометрических чисел, приводящий к исключению промежуточных веществ, называется маршрутом реакции.
В теории стационарных реакций вводятся понятия «пробег стадии», «пробег по маршруту» и «скорость реакции по базисному маршруту». Под числом пробегов стадии понимается разность числа актов элементарной реакции в прямом и обратном направлениях. Тогда скорость простой реакции равна числу ее пробегов за единицу времени в единичном реакционном пространстве. Один пробег по маршруту означает, что произошло столько пробегов каждой из стадий, каково ее стехиометрическое число для данного маршрута. В том случае, когда образование молекулы промежуточного вещества в одной из стадий скомпенсировано расходованием этой молекулы в иной стадии, реализуется стационарный режим реакции. Если в ходе этой стадии образуется не конечный продукт, а новое промежуточное вещество, то и оно должно расходоваться в другой стадии. Полная компенсация образования и расходования промежуточных веществ и означает завершение пробега по какому-либо из маршрутов.
Таким образом, скорость стационарной реакции определяется отдельными пробегами по всевозможным маршрутам. В результате все пробеги стадий за данное время окажутся однозначно определенными через базисные маршруты. Скоростью реакции по базисному маршруту называется число пробегов по базисному маршруту в единицу времени в единичном реакционном пространстве при условии, что все пробеги стадий распределены по маршрутам данного базиса. Скорость реакции в целом задается скоростями по базисным маршрутам.
Условие стационарности элементарных стадий химических реакций можно записать следующим образом:
где
 – скорости элементарных стадий (s
-й,
прямой и обратной);
– скорости элементарных стадий (s
-й,
прямой и обратной);
 –скорость по
маршруту Р
;
–скорость по
маршруту Р
;
 s
-й стадии, маршрутаР
.
s
-й стадии, маршрутаР
.
На основании уравнения (1.44) получим уравнение, которое называется уравнением стационарных реакций :
|
|
где
 ,
, ...
– скорости по маршрутам;
...
– скорости по маршрутам;
 ,
,
 .
..
– скорости элементарных стадий в прямом
и обратном направлениях;
.
..
– скорости элементарных стадий в прямом
и обратном направлениях;
 –стехиометрический
коэффициент i-
й стадии поj
-му
маршруту.
–стехиометрический
коэффициент i-
й стадии поj
-му
маршруту.
С помощью данного уравнения облегчается вывод кинетических уравнений для гетерогенных химических реакций в явном виде – для линейных механизмов и в некоторых случаях – для нелинейных.
Исследование кинетики гетерогенной химической реакции
Рассмотрим пример сложной гетерогенной химической реакции – реакции гидрокрекинга толуола.
Исходными данными являются:
детальный механизм гетерогенной химической реакции, где Z – активные центры на поверхности катализатора; Z H 2 и т. д. – адсорбированные промежуточные соединения:
|
1. H 2 + ZZH 2 2. ZH 2 + C 7 H 8 ZC 7 H 8 ∙H 2 3. ZC 7 H 8 ∙H 2 Z + C 6 H 6 +CH 4 C 7 H 8 + H 2 CH 4 + C 6 H 6 |
начальные концентрации веществ и константы скоростей, которые равны
С Н2 (0) = 0,6 мольн. доли;
С С7Н8 (0) = 0,4 мольн. доли;
 ;
;
 ;
;  ;
;
 ;
;
 ;
;  .
.
Запишем скорости элементарных стадий механизма по закону действующих поверхностей:
|
|
Математическая модель данного химического процесса будет представлять собой систему дифференциальных уравнений, выражающих изменение концентраций наблюдаемых веществ и промежуточных соединений во времени:
|
|
При решении системы дифференциальных уравнений (1.48) можно использовать численные методы Эйлера и Рунге-Кутта. Примеры результатов расчетов кинетики гетерогенной химической реакции приведены на рис. 1.5, 1.6. Программа расчета кинетики химических реакций приведена в Приложении Б.

Введение
В
кратком изложении суть представленных
в настоящей работе проблем состоит
в следующем. Развитие химии тесно
связано с построением математических
моделей. Можно сказать, что это
одна из наиболее распространенных и
информационно емких форм количественного
представления данных эксперимента.
Одна формула или значение коэффициента
в ней может квалифицированно
представлять результаты многочисленных
экспериментов.
Цели
моделирования в химии бывают
различными, от построения эмпирических
зависимостей без ограничений на
параметры и до количественной проверки
теоретических положений, для которой
как форма модели, так и значения
ее параметров должны соответствовать
физико-химическому смыслу этих положений.
В
нашей работе ставятся следующие
задачи:
-
рассмотреть основы кинетики
химических реакций на примере
гомогенных
-
примеры моделирования кинетических
уравнений на примере гомогенных
реакций
-
рассмотреть численный метод
Эйлера
-
исследовать математическую модель
протекания гомогенных реакций
-
разобрать типы моделей сложных
реакций
1 История химической кинетики
Химическая
кинетика – наука о скоростях
химических реакций, о динамическом
поведении реакционной системы
на ее пути к химическому равновесию.
Эта область физической химии
тесно связана с учением о
механизмах химических реакций, поскольку
химическая кинетика – один из методов
изучения механизмов, а механизм реакции,
как теперь стало ясно, есть основа
построения адекватной кинетической модели.
Закончился
XX век – столетие триумфального
развития химической кинетики, включающего
как микроуровень элементарного
акта, так и макроуровень многостадийных
процессов, отличающихся феноменальной
сложностью механизмов. Основы химической
кинетики как науки были заложены
в начале века работами нобелевских
лауреатов Я.Вант-Гоффа (1901 г), С.Аррениуса
(1903 г), В.Оствальда (1909 г), а также М.Боденштейна.
Различные аспекты теории элементарного
акта были развиты Г.Эйрингом, М.Поляни,
В.Г.Левичем и Р.Р.Догонадзе, лауреатами
нобелевской премии К.Фукуи и Р.Хоффманом
(1981 г), Г.Таубе (1983 г), Р.Маркусом (1992 г) и
многими другими исследователями. Теория
цепных реакций создана работами М.Боденштейна,
Й.Христиансена и нобелевских лауреатов
Н.Н.Семенова и С.Н.Хиншельвуда (1956 г), их
учеников и последователей.
Нобелевскими
премиями были отмечены методы и результаты
исследований быстрых элементарных
реакций (М.Эйген, Дж.Портер, Р.Норриш, 1967
г), а также разработка методов исследования
динамики элементарных актов газофазных
реакций (Д.Хершбах, Я.Ли, Дж.Поляни, 1986
г).
Выдающиеся
результаты были получены в области
кинетики гомогенных и гетерогенных
каталитических реакций. Отметим лишь
теорию
кинетики
гетерогенных реакций на неоднородных
поверхностях (М.И.Темкин и С.З.Рогинский),
теорию кинетики стационарных реакций
Хориути-Темкина, открытие катализа комплексами
палладия окислительных превращений олефинов
(И.И.Моисеев, М.Н.Варгафтик, Я.К.Сыркин,
Ю.Смидт и др.) и создание И.И.Моисеевым
теории этих процессов на основе детальных
кинетических исследований (премия им.
А.П.Карпинского, 1999 г).
Двадцатое
столетие увенчалось замечательным
открытием новой области физической
химии элементарного акта, названной
"фемтохимия", и нобелевской премией
по химии 1999 г американскому ученому, египтянину
А.Зевейлу (A.Zewail) "за его исследования
переходных состояний методом фемтосекундной
(10–15 сек) лазерной спектроскопии".
Достигнут предел измерения скоростей
химических реакций. Появилась возможность
следить за процессами, протекающими за
время одного колебания атомов в химической
связи – 10 – 100 фс. Переходное состояние
ряда реакций фиксируется с разрешением
0.1 A по координате реакции с полным спектральным
портретом. Достигнут уровень разрешения
соседних энергетических состояний ~10–4
см–1.
Все
результаты изучения "неравновесной"
кинетики химических реакций на микроуровне
чрезвычайно важны для обоснования
базовых принципов химической кинетики,
но пока мало полезны для решения задач
макроуровня – исследования механизмов
сложных реакций в газах, растворах и на
поверхности твердого тела в условиях
максвелл-больцмановского распределения,
т.е. задач "равновесной" кинетики
химических реакций. Если задача выяснения
механизмов и построения кинетических
моделей сложных реакций для "равновесной"
кинетики газофазных радикально-цепных
реакций решается практически (вследствие
возможности построения максимальных
механизмов или реакционных сетей с известными
константами скорости элементарных стадий),
то для сложных многомаршрутных процессов
в растворах и на поверхности решение
этой задачи только начинается. Эта проблема
XXI века.
2 Кинетика гомогенных химических реакций
Скорость химической реакции
есть изменение числа молей
реагентов в результате химического
взаимодействия в единицу времени
в единице объема (для гомогенных
реакций) или на единице поверхности
(для гетерогенных процессов) :
где С-
концентрация, моль/м 3 ,
или
Одним
из основных законов химической кинетики,
определяющим количественные закономерности
скоростей элементарных реакций, является
закон действующих масс.
Согласно
кинетическому закону действующих
масс скорость элементарной реакции при
заданной температуре пропорциональна
произведению концентраций реагирующих
веществ в степени, показывающей число
вступающих во взаимодействие частиц
(стехиометрических коэффициентов):
где
- предэкспоненциальный множитель;
E - энергия активации,
;
Т –
температура, К; R - газовая постоянная,
.
Константы
скорости реакций различного порядка
имеют разную размерность. Константа
скорости реакций первого порядка
(мономолекулярных) имеет размерность
с
-1
, константа скорости второго порядка
(бимолекулярных) – л/(моль*с).
На
основании уравнений (4) и (5) можно
записать:
-
=
(6а)
Кинетические уравнения связывают скорость реакции с параметрами, от которых она зависит. Наиболее важными из этих параметров являются концентрация, температура, давление, активность катализатора.
Рассмотрим гомогенную реакцию,
Между скоростями реакции по отдельным компонентам (обозначим их W A , W B , W C , W D) и общей скоростью реакции W существует зависимость
Чтобы применить закон действующих масс для сложной химической реакции, необходимо представить ее в виде элементарных стадий и применить этот закон к каждой стадии отдельно.
3 Примеры моделирования кинетических уравнений гомогенных химических реакций
Таким образом, кинетические модели гомогенных химических реакций представляют системы обыкновенных дифференциальных уравнений материального баланса.В результате решения системы дифференциальных уравнений получим зависимости изменения концентраций химических реагентов во времени.
- 4 Численные
методы решения кинетических уравнений
Простейшим численным методом решения обыкновенных дифференциальных уравнений является метод Эйлера. В основе этого метода лежит аппроксимация производной при малых изменениях аргумента.
Основная формула метода Эйлера имеет следующий вид
, (11)
где у i+1 – значение искомой переменной на последующем шаге;
у i – значение искомой переменной на текущем шаге;
f i – правые части дифференциального уравнения;
h – шаг интегрирования.
Например, скорость химической реакции описывается уравнением
величину называют шагом интегрирования. Решая уравнение (14), получим общую формулу Эйлера
| , | (15) |
.
Задав начальные условия: при t=0, С=С 0 , величину шага интегрирования h, а также параметры уравнения, с помощью формулы (15) можно провести пошаговый расчёт и получить решение данного уравнения (рисунок 1).
Приведем пример интегрирования первого шага системы уравнений (13) по методу Эйлера:
С А1 (t 1)= С А0 (t 0) +h· (-k·C A);
С B1 (t 1)= С B0 (t 0) +h· (k·C A);
Результаты первого шага зависят от начальной концентрации реагирующих веществ (С А0 и С B0) и величины шага h.
Организуя циклические вычисления по уравнению (15), получим для кинетической модели изменение концентраций реагирующих веществ от времени.
Величина шага интегрирования выбирается исходя из достижения минимального времени счёта и наименьшей ошибки вычислений.
Рисунок 1. Графическая иллюстрация метода Эйлера
5 Исследование кинетики гомогенных химических реакций
Исследование
кинетических закономерностей протекания
химической реакции методом математического
моделирования заключается в
определении изменения концентраций
реагирующих веществ во времени
при заданной температуре.
Пусть
протекают химические реакции
k 1
k 2
A
®
B +2C
®
D.
На
основании закона действующих масс
запишем уравнения скоростей
химических реакций и составим кинетическую
модель:
| ; ; ; ; , |
k i - константа скорости i-й химической реакции первого порядка, с -1 ; (для реакций второго порядка размерность константы ; для реакций третьего порядка размерность константы). W i - скорость i-й химической реакции, моль/л ? с; t - время реакции, с.
Систему обыкновенных дифференциальных уравнений первого порядка можно решить с использованием численного метода Эйлера, алгоритм которого записывается по уравнению (15).
Блок-схема расчета кинетики гомогенной химической реакции методом Эйлера приведена на рисунке 2.
Результаты исследования на математической модели влияния температуры на степень превращения исходного реагента и на концентрацию веществ представлены на рисунках 3,4.
Полученные результаты позволяют сделать вывод об оптимальном времени проведения процесса с целью получения целевого продукта. Математическая модель также позволяет исследовать влияние состава сырья на выход продуктов реакции.
Необходимо учитывать, что скорость химической реакции зависит от температуры, поэтому, чтобы использовать кинетическую модель для исследования процесса при различных температурах, необходимо ввести зависимость константы скорости химической реакции от температуры по уравнению Аррениуса.
Рисунок
2. Блок - схема расчета кинетики гомогенной
химической
реакции
методом Эйлера
6
Типы моделей математического
описания сложных процессов
Существует
три типа математических моделей (математического
описания) сложных процессов. Стохастические
модели используют вероятностные представления
о процессах в объекте исследования.
Вычисляются функции распределения
вероятностей для переменных параметров
модели (концентрация, температура
в случае химических процессов). Эти
модели пока что редко используются
в химической кинетике, но они оказались
полезными для описания и моделирования
поведения больших систем (химических
комплексов, химических предприятий).
Статистические модели используют для
описания эксперимента на работающем
объекте исследования. Описывается
связь значений входящих в систему
и выходящих из системы переменных
без использования физико- химической
информации о происходящих в объекте
процессах (модель черного ящика). Математическим
описанием поведения системы
обычно являются уравнения в форме
полиномов. Для обеспечения статистической
независимости параметров модели используют
планирование эксперимента (например,
ортогональные планы эксперимента). Детерминированные
модели основаны на закономерностях физико-химических
процессов с определенной структурой
модели. Именно такими моделями являются
теоретически обоснованные кинетические
модели.
При
математическом моделировании каталитического
процесса существует определенная иерархия
математических моделей. Модели первого
уровня – кинетические модели процессов
на зерне твердого катализатора или
в элементарном объеме жидкой фазы
в гомогенной реакции, неосложненные
процессами переноса массы, тепла и
гидродинамическими факторами. Модели
второго уровня в гетерогенном катализе
рассматривают процессы в слое катализатора,
а модели третьего уровня в гомогенном
и гетерогенном катализе – это
модели реактора в целом, включая все
процессы переноса и структуру потоков.
Такие модели нужны для исследования новых
реакций, для оптимизации каталитических
процессов, расчетов промышленных реакторов
(как составные части математической модели
реактора), для создания систем автоматизированного
управления процессом.
7 О понятии “механизм реакций”
Итак, в основе построения КМ лежит механизм процесса, т.е. совокупность элементарных стадий, приводящая к превращению исходных реагентов в конечные продукты реакций, причем для одной и той же реакции (каталитической или некаталитической) существует некоторое конечное множество механизмов, определяемое существующим на сегодня объемом знаний и действующими в химии парадигмами.Например, для реакции нуклеофильного замещения в ароматическом ядре ArX (некаталитической, катализируемой комплексами металлов или индуцированной переносом электронов с ArX и на ArX) установлено 8 механизмов:
Предложено 13 одномаршрутных и 80 двухмаршрутных механизмов простой реакции гидрирования этилена на металлических катализаторах. Другими словами, для каждой реакционной системы (реагенты, катализатор) существует некоторое множество элементарных стадий – реакционная сеть (максимальный механизм), отдельные блоки которой реализуются в зависимости от природы катализатора, условий, заместителей в субстрате, степени окисления металла-катализатора.
В конце столетия наметилось объединение физико-химического и формально-кинетического подходов в изучении механизмов. Был сформулирован взгляд на механизм как на единство двух составляющих этого понятия – топологической (структурной) и химической составляющих, и на их равноправие – нельзя однозначно установить структуру механизма (взаимосвязь элементарных стадий) на основе только формально-кинетического описания, так называемую "схему механизма", а потом наполнить ее химическим содержанием. Нельзя в общем случае из кинетических экспериментов получить информацию, необходимую для корректной идентификации схемы механизма, не задав этот механизм и не поставив соответствующие задачи для формально-кинетического метода.
Все эти обстоятельства вызвали необходимость пересмотра традиционной стратегии построения КМ.
8 Альтернативные стратегии моделирования КМ
Традиционная процедура построения КМ включает следующие этапы:Главный недостаток этой процедуры (стратегии) – отсутствие алгоритмов однозначного выполнения всех этапов. Поскольку эксперимент может быть адекватно описан большим числом математических моделей (уравнений), исследователь должен иметь какую-либо гипотезу о схеме механизма (о структуре механизма) или о форме предполагаемых уравнений. При этом подбор возможных гипотез (иногда интуитивный) происходит уже после сделанного эксперимента. Нет алгоритма перехода от математической модели к физической модели (особенно для многомаршрутных реакций) (этап (б)). Переход к механизму реакции (этап (в)) также произволен и не формализован. На всех этапах этой стратегии присутствует естественное стремление получить хотя бы одно уравнение (и "схему механизма"), не противоречащее эксперименту, и, очень часто, ни о какой дискриминации набора гипотез не идет речи. Напротив, авторы такой схемы механизма начинают ставить эксперименты, чтобы доказать механизм, представляющийся автору наиболее разумным. Вместе с тем, уже давно установлено, что доказать какую-либо гипотезу нельзя. Можно доказательно отбросить неработающие гипотезы и показать согласие с экспериментом оставшихся гипотез – множества работающих гипотез. Целесообразность выдвижения набора гипотез и получение множества работающих гипотез была убедительно обоснована более 100 лет назад американским ученым-геологом Т.Чемберленом.
Таким образом, рациональная стратегия построения КМ является четкой методологически обоснованной гипотетико-дедуктивной логической схемой исследования, поддержанной возможностями компьютеров и эффективным программным обеспечением. Суть этой стратегии отражена в последовательности ее этапов:
Дискриминация
гипотез может включать дискриминацию
стадий, блоков стадий, отдельных механизмов,
узлов сопряжения в многомаршрутных
реакциях.
Вид
КМ (формы математического описания)
зависит от особенностей механизма
(линейный или нелинейный), условий
проведения процесса (стационарный, квазистационарный,
нестационарный), типа реактора (открытый,
закрытый) и ряда принятых допущений.
Линейным механизмом называют механизм,
элементарные стадии которого в прямом
и обратном направлениях линейны
по интермедиатам – только одно
промежуточное соединение находится
слева (или справа) от стрелки в
элементарной стадии. Если в стадии
участвует больше одного интермедиата
(в том числе и 2 молекулы одного
интермедиата), стадии нелинейны и
механизм нелинейный.
Самым
общим видом КМ являются системы
дифференциальных уравнений, алгебро-дифференциальных
или алгебраических уравнений
,
(16)
правая
часть которых всегда есть произведение
матрицы стехиометрических коэффициентов
для стадий механизма (транспонированной)
на вектор-столбец скоростей элементарных
стадий (). В случае линейных механизмов для
реакции в стационарных или квазистационарных
условиях правая часть уравнения (1) преобразуется
в дробно-рациональные уравнения скоростей
по реагентам (R
i
) или скоростей
по маршрутам (R
p
). Системы
алгебраических уравнений для нелинейных
механизмов в общем случае не решаются,
и уравнения типа (16) не приводятся к более
простому дробно-рациональному виду.
В
случае кинетики на неоднородных поверхностях
в стационарных условиях скорость может
описываться и степенным уравнением
типа (17) (уравнение М.И.Темкина для синтеза
аммиака):
(17)
Коэффициент
m
= 0.5 в случае железного катализатора,
k
+ /k
– = K
– константа
равновесия реакции
Под прямой задачей химической кинетики понимают задачу нахождения концентраций участвующих в реакции веществ в любой момент времени, исходя из известных начальных концентраций, схемы реакции и констант скоростей отдельных стадий. Обратная задача химической кинетики - восстановление поизвестной зависимости концентрации веществ от времени схемы реакции и констант скорости.
9.1 Классификация обратных задач
Формальная
кинетика гомогенных химических реакций
основана на двух основныхпостулатах.
Согласно (кинетическому) закону действия
масс скорость элементарной стадии пропорциональна
концентрации участвующих в ней реагентов.
Коэффициент
пропорциональности и называется константой
скорости. Согласно принципу независимого
протекания отдельных стадий скорость
реакции не зависитот протекания в данный
момент в системе других химических реакций.
Такимобразом, зная схему реакции, легко
записать систему обыкновенных дифференциальных
уравнений, отражающую изменение концентрации
всехучаствующих в реакции веществ во
времени:
d
c/dt
= f
(k, c)
(18)
где с -
вектор концентраций веществ, k - вектор
констант скоростей отдельных стадий,
вид функции f
определяется схемой
реакции.
Интегрируя
эту систему аналитически либо численно,
получаем:
с = F(k, c 0 ,
t
)
(19)
где с 0
- вектор начальных концентраций веществ.
Пользуясь
введенными выше обозначениями, можно
выделить несколько ступеней в решении
обратной задачи.
Нулевая
ступень - проверка адекватности.
На ней дается ответ на вопрос, соответствуют
ли экспериментально наблюдаемые кривые
c(t) рассчитанным с использованием текущей
модели f и констант k.
Первая
ступень - параметрическая идентификация.
На этой ступени
находится
набор констант k, наилучшим образом
описывающий экспериментальные кривые
c
(t
) в рамках данной модели f
.
Понятно, что успешное решение задачи
первой ступени возможно, только опираясь
на нулевую ступень.
Вторая
ступень - структурная идентификация.
Выбор модели f
, соответствующей действительно
происходящей химической реакции, который
делается на основе решения задачи первой
ступени с привлечением других сведений
о механизме данной реакции.
.
9.2
Проверка адекватности и параметрическая
идентификация
В
случае достаточно простой схемы
реакции, когда возможно получение
функции c
(t
) в явном виде, проверка
адекватности сводится к вычислению теоретических
значений функции при различных значениях
времени и сравнении их с экспериментальными.
К сожалению, часто системы дифференциальных
уравнений, описывающие сложные химические
реакции, не могут быть проинтегрированы
в аналитическом виде, и приходится прибегать
к численным методам интегрирования.
и т.д.................
 ,
, ,
, ,
,
 ;
;
 ;
; ;
; ;
.
;
.