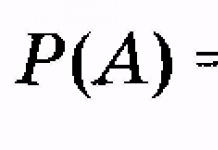Виды уравнений и способы их решения. Реферат: Уравнения и способы их решения Какие виды уравнений

Что такое уравнение?

Тем, кто делает первые шаги в алгебре, конечно, требуется максимально упорядоченная подача материала. Поэтому в нашей статье о том, что такое уравнение, мы не только дадим определение, но и приведём различные классификации уравнений с примерами.

Что такое уравнение: общие понятия

Итак, уравнение — это вид равенства с неизвестным, обозначаемым латинской буквой. При этом числовое значение данной буквы, позволяющее получить верное равенство, называется корнем уравнения.Более подробно об этом вы можете прочитать в нашей статье , мы же продолжим разговор о самих уравнениях. Аргументами уравнения (или переменными) называются неизвестные, а решением уравнения называется нахождение всех его корней либо отсутствия корней.

Виды уравнений

Уравнения подразделяются на две большие группы: алгебраические и трансцендентные.

• Алгебраическим называется такое уравнение, в котором для нахождения корня уравнения используются только алгебраические действия - 4 арифметических, а также возведение в степень и извлечение натурального корня.
• Трансцендентным называется уравнение, в котором для нахождения корня используются неалгебраические функции: например, тригонометрические, логарифмические и иные.

Среди алгебраических уравнений выделяют также:

• целые — с обеими частями, состоящими из целых алгебраических выражений по отношению к неизвестным;
• дробные — содержащие целые алгебраические выражения в числителе и знаменателе;
• иррациональные — алгебраические выражения здесь находятся под знаком корня.

Заметим также, что дробные и иррациональные уравнения можно свести к решению целых уравнений.

Трансцендентные уравнения подразделяются на:

• показательные — это такие уравнения, которые содержат переменную в показателе степени. Они решаются путём перехода к единому основанию или показателю степени, вынесением общего множителя за скобку, разложением на множители и некоторыми другими способами;
• логарифмические — уравнения с логарифмами, то есть такие уравнения, где неизвестные находятся внутри самих логарифмов. Решать такие уравнения весьма непросто (в отличие от, допустим, большинства алгебраических), поскольку для этого требуется солидная математическая подготовка. Самое важное здесь — перейти от уравнения с логарифмами к уравнению без них, то есть упростить уравнение (такой способ удаления логарифмов называется потенцированием). Разумеется, потенцировать логарифмическое уравнение можно только в том случае, если они имеют тождественные числовые основания и не имеют коэффициентов;
• тригонометрические — это уравнения с переменных под знаками тригонометрических функций. Их решение требует первоначального освоения тригонометрических функций;
• смешанные — это дифференцированные уравнения с частями, принадлежащими к различным типам (например, с параболической и эллиптической частями или эллиптической и гиперболической и т.д.).

Что касается классификации по числу неизвестных, то здесь всё просто: различают уравнения с одним, двумя, тремя и так далее неизвестными. Существует также и ещё одна классификация, которая основывается на степени, которая имеется в левой части многочлена. Исходя из этого различают линейные, квадратные и кубические уравнения. Линейные уравнения также могут называться уравнениями 1-й степени, квадратные — 2-й, а кубические, соответственно, 3-й. Ну а теперь приведём примеры уравнений той или иной группы.

Примеры различных типов уравнений

Примеры алгебраических уравнений:

• ax + b= 0
• ax 3 + bx 2 + cx+ d= 0
• ax 4 + bx 3 + cx 2 + bx + a= 0
  (a не равно 0)

Примеры трансцендентных уравнений:

• cos x = x lg x = x−5 2 x = lgx+x 5 +40

Примеры целых уравнений:

• (2+x)2 = (2+x)(55x-4) (x2-12x+10)4 = (3x+10)4 (4x2+3x-10)2=9x4

Пример дробных уравнений:

• 15 x + — = 5x - 17 x

Пример иррациональных уравнений:

• √2kf(x)=g(x)

Примеры линейных уравнений:

• 2х+7=0 х - 3 = 2 - 4х 2х+3=5х+5 - 3х - 2

Примеры квадратных уравнений:

• x 2 +5x−7= 0 3x 2 +5x−7= 0 11x 2 −7x+3 = 0

Примеры кубических уравнений:

• x 3 -9x 2 -46x+120=0 x 3 - 4x 2 + x + 6 = 0

Примеры показательных уравнений:

• 5 х+2 = 125 3 х ·2 х = 8 х+3 3 2х +4·3 х -5 = 0

Примеры логарифмических уравнений:

• log 2 x= 3 log 3 x= -1

Примеры тригонометрических уравнений:

• 3sin 2 x + 4sin x cosx + cos 2 x = 2 sin(5x+π/4) = ctg(2x-π/3) sinx + cos 2 x + tg 3 x = ctg 4 x

Примеры смешанных уравнений:

• log х (log 9 (4⋅3 х −3))=1 |5x−8|+|2⋅5x+3|=13

Осталось добавить, что для решения уравнений различных типов применяются самые разные методы. Ну а чтобы решать практически любые уравнения, потребуются знания не только алгебры, но также и тригонометрии, причём нередко знания весьма глубокие.

В курсе школьной математики, ребенок впервые слышит термин "уравнение". Что такое это, попробуем разобраться вместе. В данной статье рассмотрим виды и способы решения.

Математика. Уравнения

Для начала предлагаем разобраться с самим понятием, что это такое? Как гласят многие учебники математики, уравнение - это некоторые выражения, между которыми стоит обязательно знак равенства. В этих выражениях присутствуют буквы, так называемые переменные, значение которых и необходимо найти.

Это атрибут системы, который меняет свое значение. Наглядным примером переменных являются:

• температура воздуха;
• рост ребенка;
• вес и так далее.

В математике они обозначаются буквами, например, х, а, b, с... Обычно задание по математике звучит следующим образом: найдите значение уравнения. Это значит, что необходимо найти значение данных переменных.

Разновидности

Уравнение (что такое, мы разобрали в предыдущем пункте) может быть следующего вида:

• линейные;
• квадратные;
• кубические;
• алгебраические;
• трансцендентные.

Для более подробного знакомства со всеми видами, рассмотрим каждый в отдельности.

Линейное уравнение

Это первый вид, с которым знакомятся школьники. Они решаются довольно-таки быстро и просто. Итак, линейное уравнение, что такое? Это выражение вида: ах=с. Так не особо понятно, поэтому приведем несколько примеров: 2х=26; 5х=40; 1,2х=6.

Разберем примеры уравнений. Для этого нам необходимо все известные данные собрать с одной стороны, а неизвестные в другой: х=26/2; х=40/5; х=6/1,2. Здесь использовались элементарные правила математики: а*с=е, из этого с=е/а; а=е/с. Для того чтобы завершить решение уравнения, выполним одно действие (в нашем случае деление) х=13; х=8; х=5. Это были примеры на умножение, теперь просмотрим на вычитание и сложение: х+3=9; 10х-5=15. Известные данные переносим в одну сторону: х=9-3; х=20/10. Выполняем последнее действие: х=6; х=2.

Также возможны варианты линейных уравнений, где используется более одной переменной: 2х-2у=4. Для того чтобы решить, необходимо к каждой части прибавить 2у, у нас получается 2х-2у+2у=4-2у, как мы заметили, по левую часть знака равенства -2у и +2у сокращаются, при этом у нас остается: 2х=4-2у. Последним шагом делим каждую часть на два, получаем ответ: икс равен два минус игрек.

Задачи с уравнениями встречаются даже на папирусах Ахмеса. Вот одна из задач: число и четвертая его часть дают в сумме 15. Для ее решения мы записываем следующее уравнение: икс плюс одна четвертая икс равняется пятнадцати. Мы видим еще один пример по итогу решения, получаем ответ: х=12. Но эту задачу можно решить и другим способом, а именно египетским или, как его называют по-другому, способом предположения. В папирусе используется следующее решение: возьмите четыре и четвертую ее часть, то есть единицу. В сумме они дают пять, теперь пятнадцать необходимо разделить на сумму, мы получаем три, последним действием три умножаем на четыре. Мы получаем ответ: 12. Почему мы в решении пятнадцать делим на пять? Так узнаем, во сколько раз пятнадцать, то есть результат, который нам необходимо получить, меньше пяти. Таким способом решали задачи в средние века, он стал зваться методом ложного положения.

Квадратные уравнения

Кроме рассмотренных ранее примеров, существуют и другие. Какие именно? Квадратное уравнение, что такое? Они имеют вид ax 2 +bx+c=0. Для их решения необходимо ознакомиться с некоторыми понятиями и правилами.

Во-первых, нужно найти дискриминант по формуле: b 2 -4ac. Есть три варианта исхода решения:

• дискриминант больше нуля;
• меньше нуля;
• равен нулю.

В первом варианте мы можем получить ответ из двух корней, которые находятся по формуле: -b+-корень из дискриминанта разделенные на удвоенный первый коэфициент, то есть 2а.

Во втором случае корней у уравнения нет. В третьем случае корень находится по формуле: -b/2а.

Рассмотрим пример квадратного уравнения для более подробного знакомства: три икс в квадрате минус четырнадцать икс минус пять равняется нулю. Для начала, как и писалось ранее, ищем дискриминант, в нашем случае он равен 256. Отметим, что полученное число больше нуля, следовательно, мы должны получить ответ состоящих из двух корней. Подставляем полученный дискриминант в формулу нахождения корней. В результате мы имеем: икс равняется пяти и минус одной третьей.

Особые случаи в квадратных уравнениях

Это примеры, в которых некоторые значения равны нулю (а, b или с), а возможно и несколько.

Для примера возьмем следующее уравнение, которое является квадратным: два икс в квадрате равняется нулю, здесь мы видим, что b и с равны нулю. Попробуем его решить, для этого обе части уравнения делим на два, мы имеем: х 2 =0. В итоге получаем х=0.

Другой случай 16х 2 -9=0. Здесь только b=0. Решим уравнение, свободный коэфициент переносим в правую часть: 16х 2 =9, теперь каждую часть делим на шестнадцать: х 2 = девять шестнадцатых. Так как у нас х в квадрате, то корень из 9/16 может быть как отрицательным, так и положительным. Ответ записываем следующим образом: икс равняется плюс/минус три четвертых.

Возможен и такой вариант ответа, как у уравнения корней вовсе нет. Посмотрим на такой пример: 5х 2 +80=0, здесь b=0. Для решения свободный член перекидываете в правую сторону, после этих действий получаем: 5х 2 =-80, теперь каждую часть делим на пять: х 2 = минус шестнадцать. Если любое число возвести в квадрат, то отрицательное значение мы не получим. По этому наш ответ звучит так: у уравнения корней нет.

Разложение трехчлена

Задание по квадратным уравнениям может звучать и другим образом: разложить квадратный трехчлен на множители. Это возможно осуществить, воспользовавшись следующей формулой: а(х-х 1)(х-х 2). Для этого, как и в другом варианте задания, необходимо найти дискриминант.

Рассмотрим следующий пример: 3х 2 -14х-5, разложите трехчлен на множетели. Находим дискриминант, пользуясь уже известной нам формулой, он получается равным 256. Сразу отмечаем, что 256 больше нуля, следовательно, уравнение будет иметь два корня. Находим их, как в предыдущем пункте, мы имеем: х= пять и минус одна третья. Воспользуемся формулой для разложения трехчлена на множетели: 3(х-5)(х+1/3). Во второй скобке мы получили знак равно, потому что в формуле стоит знак минуса, а корень тоже отрицательный, пользуясь элементарными знаниями математики, в сумме мы имеем знак плюса. Для упрощения, перемножим первый и третий член уравнения, чтобы избавиться от дроби: (х-5)(х+1).

Уравнения сводящиеся к квадратному

В данном пункте научимся решать более сложные уравнения. Начнем сразу с примера:

(x 2 - 2x) 2 - 2(x 2 - 2x) - 3 = 0. Можем заметить повторяющиеся элементы: (x 2 - 2x), нам для решения удобно заменить его на другую переменную, а далее решать обычное квадратное уравнение, сразу отмечаем, что в таком задании мы получим четыре корня, это не должно вас пугать. Обозначаем повторение переменной а. Мы получаем: а 2 -2а-3=0. Наш следующий шаг - это нахождение дискриминанта нового уравнения. Мы получаем 16, находим два корня: минус один и три. Вспоминаем, что мы делали замену, подставляем эти значения, в итоге мы имеем уравнения: x 2 - 2x=-1; x 2 - 2x=3. Решаем их в первом ответ: х равен единице, во втором: х равен минусу одному и трем. Записываем ответ следующим образом: плюс/минус один и три. Как правило, ответ записывают в порядке возрастания.

Кубические уравнения

Рассмотрим еще один возможный вариант. Речь пойдет о кубических уравнениях. Они имеют вид: ax 3 + b x 2 + cx + d =0. Примеры уравнений мы рассмотрим далее, а для начала немного теории. Они могут иметь три корня, так же существует формула для нахождения дискриминанта для кубического уравнения.

Рассмотрим пример: 3х 3 +4х 2 +2х=0. Как его решить? Для этого мы просто выносим х за скобки: х(3х 2 +4х+2)=0. Все что нам остается сделать - это вычислить корни уравнения в скобках. Дискриминант квадратного уравнения в скобках меньше нуля, исходя из этого, выражение имеет корень: х=0.

Алгебра. Уравнения

Переходим к следующему виду. Сейчас мы кратко рассмотрим алгебраические уравнения. Одно из заданий звучит следующим образом: разложить на множетели 3х 4 +2х 3 +8х 2 +2х+5. Самым удобным способом будет следующая группировка: (3х 4 +3х 2)+(2х 3 +2х)+(5х 2 +5). Заметим, что 8х 2 из первого выражения мы представили в виде суммы 3х 2 и 5х 2 . Теперь выносим из каждой скобки общий множитель 3х 2 (х2+1)+2х(х 2 +1)+5(х 2 +1). Мы видим, что у нас есть общий множитель: икс в квадрате плюс один, выносим его за скобки: (х 2 +1)(3х 2 +2х+5). Дальнейшее разложение невозможно, так как оба уравнения имеют отрицательный дискриминант.

Трансцендентные уравнения

Предлагаем разобраться со следующим типом. Это уравнения, которые содержат трансцендентные функции, а именно логарифмические, тригонометрические или показательные. Примеры: 6sin 2 x+tgx-1=0, х+5lgx=3 и так далее. Как они решаются вы узнаете из курса тригонометрии.

Функция

Завершающим этапом рассмотрим понятие уравнение функции. В отличии от предыдущих вариантов, данный тип не решается, а по нему строится график. Для этого уравнение стоит хорошо проанализировать, найти все необходимые точки для построения, вычислить точку минимума и максимума.

В алгебре рассматриваются два вида равенств – тождества и уравнения.

Тождество – это равенство, которое выполняется при всех (допустимых) значениях входящих в него букв.

Уравнение – это равенство, которое выполняется лишь при некоторых значениях входящих в него букв.

Буквы, входящие в уравнение, могут быть неравноправными: одни могут принимать все свои допустимые значения, которые называют коэффициентами (иногда – параметрами) уравнения, другие, значения которых требуется отыскать, называют неизвестными данного уравнения (как правило, их обозначают последними буквами латинского алфавита x, y, z, u, v, w, или теми же буквами, снабженными индексами.

Уравнения бывают:
Квадратные уравнения
Рациональные уравнения
Уравнения, содержащие переменную под знаком модуля
Иррациональные уравнения
Показательные уравнения
Логарифмические уравнения

Системы уравнений:
Системы рациональных уравнений
Системы нелинейных уравнений
Симметрические системы
Смешанные системы

Посторонние корни, возникшие в процессе преобразований, можно выявить проверкой. Конечно, если все преобразования приводили нас к цепочке равносильных уравнений, то проверка необязательна. Однако этого не всегда можно добиться, легче следить за тем, чтобы каждое уравнение цепочки являлось следствием предыдущего, т.е. чтобы не происходила потеря корней. В этом случае проверка является элементом решения. Следует отметить, что часто легче сделать проверку, чем обосновать то, что в ней нет необходимости. Кроме того, проверка является средством контроля правильности проделанных вычислений. Иногда полезно поступать так: на каждом этапе решения уравнения определять промежутки, в которых могут находиться корни уравнения. Все корни, не принадлежащие этим промежуткам, являются посторонними и должны быть отброшены. Однако остальные корни всё равно необходимо проверить подстановкой в исходное уравнение.

Каждое алгебраическое уравнение всегда имеет хотя бы одно решение, действительное или комплексное.

В аналитической геометрии одно уравнение с двумя неизвестными интерпретируется при помощи кривой на плоскости, координаты всех точек которой удовлетворяют данному Уравнению. Одно Уравнение с тремя неизвестными интерпретируется при помощи поверхности в трёхмерном пространстве. При этой интерпретации решение системы Уравнение совпадает с задачей о разыскании точек пересечения линий, поверхностей и т.д. Уравнение с большим числом неизвестных интерпретируются при помощи многообразий в n-мерных пространствах.

Добро пожаловать!

Уравнения математической физики - дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные и т.д.), к которым приводит математический анализ физических явлений. Для теории Уравнения математической физики характерна постановка задач в таком виде, как это необходимо при исследовании физического явления. Круг Уравнения математической физики с расширением области применения математического анализа также неуклонно расширяется. При систематизации полученных результатов появляется необходимость включить в теорию Уравнения математической физики уравнения и задачи более общего вида, чем те, которые появляются при анализе конкретных явлений; однако и для таких уравнений и задач характерно то, что их свойства допускают более или менее наглядное физическое истолкование.

Уравнения химические - изображения реакций химических посредством знаков химических, формул химических, чисел и математических знаков. На возможность такого описания химических реакций указал в 1789 А. Лавуазье, основываясь на сохранения массы законе; однако всеобщее применение Уравнения химические получили только в 1-й половине 19 в.

уравнение неравенство математика

Понятие «уравнение » относится к важнейшим общематематическим понятиям.

Существуют различные трактовки понятия «уравнение».

И.Я. Виленкин и др. приводит логико - математическое определение уравнения. Пусть на множестве М зафиксирован набор алгебраических операций, х - переменная на М; тогда уравнением на множестве М относительно x называется предикат вида, где и - термы относительно заданных операций, в запись которого входит символ.Аналогично определиться уравнение от двух и более переменных.

Принятые в логики термины «терм» и «предикат» соответствуют такие термины школьной математики как «выражение» и «предложение с переменной». Поэтому наиболее близко к приведенному формальному определению можно считать следующее определение: «Предложение с переменной, имеющий вид равенства между двумя выражениями с этой переменной, называется уравнением». Такое определение приведено в учебнике «Алгебра и начала анализа» А.Н Колмогоров и др. Равенство с переменной называется уравнением. Значение переменной при котором равенство с переменной обращается в верное числовое равенство, называется корнем уравнения.

Часто, особенно в начале систематического курса алгебры, понятие уравнение вводится по средством выделение его из алгебраического метода решения задач. Например, в учебнике Ш.А.Алимова и др. понятие уравнение вводиться на материале текстовой задачи. Переход к понятию уравнения осуществляется на основе анализа некоторых формальных особенностей записи, выражающих содержание данной задачи в алгебраической форме: «Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением». Указываемый способ введения понятия уравнения соответствует еще одному компоненту понятия уравнения - прикладному.

Еще один подход к понятию уравнения получается при составления области определения уравнения и множества его корней. Например, в учебнике Д.К.Фадеева «Буквенное равенство, которое не обязательно превращается в верное числовое равенство при допустимых наборов букв, называется уравнение».

Можно встретить и третий вариант определения, роль которого проявляется при изучения графического метода решения уравнений: «Уравнение - это равенство двух функций».

Среди всех изучаемых в курсе математике типов уравнений В.И. Мишин выделяет сравнительно ограничение количество основных типов. к их числу относится: линейное уравнение с одним неизвестным, систему двух линейных уравнений с двумя неизвестными, квадратные уравнения, простейшие иррациональные и трансцендентные.

Ю.М.Колягин и др. классифицируют по виду функций, представляющих правую и левую части уравнений:

Уравнение называется:

алгебраическим, если и - алгебраические функции;

трансцендентным, если хотя одним из функций и трансцендентная;

рациональным алгебраическим (или просто рациональным) , если алгебраические функции и рациональные;

иррациональным алгебраическим(или просто иррациональным), если хотя бы одна из алгебраических функций и иррациональная;

целым рациональным, если функция и целые рациональные;

дробным рациональным, если хотя бы одна из рациональных функций и дробная рациональная.

Уравнение, где - многочлен стандартного вида, называется линейным (первой степени), квадратным(во второй степени), кубическим (третьей степени) и вообще - ой степени, если многочлен, имеет соответственно первую, вторую, третью и вообще - ую степень.

В школе изучаются несколько типов уравнений. К их числу относятся: линейные уравнения с одной не известной, квадратные уравнения, иррациональные и трансцендентные уравнения, рациональные уравнения. Эти типы уравнений изучаются с большой тщательностью, для них указывается и доводиться до автоматизма выполнение алгоритма решения, указывается форма, в котором должен записываться ответ.

Виды уравнений и методы решения:

1) Линейное уравнение

Уравнением с одной переменной, называется равенство, содержащее только одну переменную.

Корнем (или решением) уравнения называется такое значение переменной, при котором уравнение превращается в верное числовое равенство.

Найти все корни уравнения или доказать, что их нет - это значит решить уравнение.

Пример 1: Решить уравнение.

2) Квадратное уравнение

Квадратное уравнение -- это уравнение вида, где коэффициенты a, b и c - любые действительные числа, причем а?0.

Корнями квадратного уравнения называют такие значения переменной, при которых квадратное уравнение обращается в верное числовое равенство.

Решить квадратное уравнение - значит найти все его корни или установить, что корней нет.

Пример 2: Решить уравнение

Данное уравнение можно решить либо через Теорему Виета, либо через дискриминант.

Ответ: х 1 =-1, х 2 =-2.

3) Рациональные уравнения

рациональные уравнения - уравнения вида

где и многочлены, атак же уравнения вида, где и - рациональные.

Пример 3: Решить уравнение

4) Иррациональные уравнения

Иррациональные уравнения - это уравнения, в которых переменная содержится под знаком корня или под знаком операции возведения в дробную степень.

Пример 4: Решить уравнение

Возведем обе части в квадрат:

5) Показательные и логарифмические уравнения

При решения показательных уравнений используются два основных метода: а) переход от уравнения к уравнению;б) введения новых переменных. Иногда приходиться применять исскуственные приемы.

Логарифмические уравнения - решаются тремя методами, то есть переход от уравнения к уравнению - следствию;метод введения новых переменных логарифмирования, то есть переход от уравнения к уравнению.

А так же во многих случаях при решения логарифмического уравнения приходиться использовать свойства логарифма произведения, частного, степени, корня.

Министерство общего и профессионального образования РФ

Муниципальное образовательное учреждение

Гимназия № 12

сочинение

на тему: Уравнения и способы их решения

Выполнил: ученик 10 "А" класса

Крутько Евгений

Проверила: учитель математики Исхакова Гульсум Акрамовна

Тюмень 2001

План................................................................................................................................... 1

Введение........................................................................................................................... 2

Основная часть................................................................................................................. 3

Заключение..................................................................................................................... 25

Приложение................................................................................................................... 26

Список использованной литературы.......................................................................... 29

План.

Введение.

Историческая справка.

Уравнения. Алгебраически уравнения.

а) Основные определения.

б) Линейное уравненение и способ его решения.

в) Квадратные уравнения и способы его решения.

г) Двучленные уравнения способ их решения.

д) Кубические уравнения и способы его решения.

е) Биквадратное уравнение и способ его решения.

ё) Уравнения четвертой степени и способы его решения.

ж) Уравнения высоких степеней и способы из решения.

з) Рациональноное алгебраическое уравнение и способ его

и) Иррациональные уравнения и способы его решения.

к) Уравнения, содержащие неизвестное под знаком.

абсолютной величины и способ его решения.

Трансцендентные уравнения.

а) Показательные уравнения и способ их решения.

б) Логарифмические уравнения и способ их решения.

Введение

Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека. Практически все, что окружает современного человека – это все так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать.

Данная работа является попыткой обобщить и систематизировать изученный материал по выше указанной теме. Я расположил материал по степени его сложности, начиная с самого простого. В него вошли как известные нам виды уравнений из школьного курс алгебры, так и дополнительный материал. При этом я попытался показать виды уравнений, которые не изучаются в школьном курсе, но знание которых может понадобиться при поступлении в высшее учебное заведение. В своей работе при решении уравнений я не стал ограничиваться только действительным решением, но и указал комплексное, так как считаю, что иначе уравнение просто недорешено. Ведь если в уравнении нет действительных корней, то это еще не значит, что оно не имеет решений. К сожалению, из-за нехватки времени я не смог изложить весь имеющийся у меня материал, но даже по тому материалу, который здесь изложен, может возникнуть множество вопросов. Я надеюсь, что моих знаний хватит для того, чтобы дать ответ на большинство вопросов. Итак, я приступаю к изложению материала.

Математика... выявляет порядок,

симметрию и определенность,

а это – важнейшие виды прекрасного.

Аристотель.

Историческая справка

В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. "Ищется куча, которая вместе с двумя третями ее, половиной и одной седьмой составляет 37...", - поучал во II тысячелетии до новой эры египетский писец Ахмес. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.

Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: "Смотри!", "Делай так!", "Ты правильно нашел". В этом смысле исключением является "Арифметика" греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений.

Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово "аль-джебр" из арабского названия этого трактата – "Китаб аль-джебер валь-мукабала" ("Книга о восстановлении и противопоставлении") – со временем превратилось в хорошо знакомое всем слово "алгебра", а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.

уравнения. Алгебраические уравнения

Основные определения

В алгебре рассматриваются два вида равенств – тождества и уравнения.

Тождество – это равенство, которое выполняется при всех (допустимых) значениях входящих в него букв ). Для записи тождества наряду со знаком

Уравнение – это равенство, которое выполняется лишь при некоторых значениях входящих в него букв. Буквы, входящие в уравнение, по условию задачи могут быть неравноправны: одни могут принимать все свои допустимые значения (их называют параметрами или коэффициентами уравнения и обычно обозначают первыми буквами латинского алфавита:

В общем виде уравнение может быть записано так:

В зависимости от числа неизвестных уравнение называют уравнением с одним, двумя и т. д. неизвестными.

Значение неизвестных, обращающие уравнение в тождество, называют решениями уравнения.

Решить уравнение – это значит найти множество его решений или доказать, что решений нет. В зависимости от вида уравнения множество решений уравнения может быть бесконечным, конечным и пустым.

Если все решения уравнения